机考E卷200分题 - 最大相连男生数学生方阵
题目描述
学校组织活动,将学生排成一个矩形方阵。
请在矩形方阵中找到最大的位置相连的男生数量。
这个相连位置在一个直线上,方向可以是水平的,垂直的,成对角线的或者呈反对角线的。
注:学生个数不会超过10000
输入描述
输入的第一行为矩阵的行数和列数,接下来的n行为矩阵元素,元素间用”,”分隔。
输出描述
输出一个整数,表示矩阵中最长的位置相连的男生个数。
示例1
输入
3,4
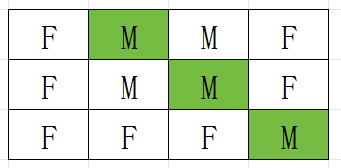
F,M,M,F
F,M,M,F
F,F,F,M
1234
输出
3
1
说明
解题思路
题目要求在一个由学生组成的矩形方阵中,找到最大的位置相连的男生数量。这里“相连”是指男生的所在位置可以通过水平、垂直、对角线或反对角线方向连续连接。
代码思路
- 遍历整个方阵中的每个元素,当找到一个男生
M时,调用getMaxConnected方法,开始从该位置搜索最长连续的M数量。 getMaxConnected方法实现了四个方向的搜索(水平、垂直、对角线、反对角线):- 水平(从左往右):从当前位置向右方向扫描,计算连续的
M数量。 - 垂直(从上往下):从当前位置向下方向扫描,计算连续的
M数量。 - 对角线(左上到右下):从当前位置向右下方向扫描,计算连续的
M数量。 - 反对角线(右上到左下):从当前位置向左下方向扫描,计算连续的
M数量。
- 水平(从左往右):从当前位置向右方向扫描,计算连续的
- 每找到一条连续的男生
M,将其数量添加到结果列表res中。
示例解释
给定输入:
3,4
F,M,M,F
F,M,M,F
F,F,F,M
1234
-
构建的矩阵为:
F M M F F M M F F F F M 123 -
逐个扫描矩阵,当扫描到
M时(如[0,1]位置的M),开始四个方向的搜索。- 水平:
M(0,1) 和 (0,2),长度为2 - 垂直:
M(0,1), (1,1),长度为2 - 对角线:
M(0,1),只有一个 - 反对角线:
M(0,2), (1,3),长度为2
- 水平:
-
将结果存入
max_res,最后在整个矩阵中找到的最大连续M的数量是3(在对角线方向上)。
最终输出结果为3。
提示,为了让大家看的更明白,代码把各个方向的搜索都拆开了,其实可以放在一起,详见对应代码
Java
import java.util.*;
public class Main {
public static void getMaxConnected(List<List<String>> students, int row, int column, List<Integer> res) {
int len = 1; // 初始化连续的M的个数为1
int a = 0, b = 0; // 初始化行和列的索引
int m = students.size(), n = students.get(0).size(); // 获取方阵的行数和列数
if (column < n) { // 从左往右搜索
a = row;
b = column;
while (b < n - 1 && students.get(a).get(++b).equals("M")) { // 不越界且下一个元素为M
len++; // 连续的M的个数加1
}
res.add(len); // 把连续的M的个数加入结果数组
len = 1; // 重新初始化连续的M的个数为1
}
if (row < m) { // 从上往下搜索
a = row;
b = column;
while (a < m - 1 && students.get(++a).get(b).equals("M")) { // 不越界且下一个元素为M
len++; // 连续的M的个数加1
}
res.add(len); // 把连续的M的个数加入结果数组
len = 1; // 重新初始化连续的M的个数为1
}
if (row < m && column < n) { // 对角线搜索
a = row;
b = column;
while ((a < m - 1 && b < n - 1) && students.get(++a).get(++b).equals("M")) { // 不越界且下一个元素为M
len++; // 连续的M的个数加1
}
res.add(len); // 把连续的M的个数加入结果数组
len = 1; // 重新初始化连续的M的个数为1
}
if (row >= 0 && column < n) { // 从右往左搜索
a = row;
b = column;
while ((a > 0 && b < n - 1) && students.get(--a).get(++b).equals("M")) { // 不越界且下一个元素为M
len++; // 连续的M的个数加1
}
res.add(len); // 把连续的M的个数加入结果数组
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 读取矩阵大小
String[] dimensions = scanner.nextLine().split(",");
int row = Integer.parseInt(dimensions[0]);
int column = Integer.parseInt(dimensions[1]);
// 初始化方阵
List<List<String>> students = new ArrayList<>();
for (int i = 0; i < row; i++) {
String[] lineElements = scanner.nextLine().split(",");
students.add(Arrays.asList(lineElements));
}
List<Integer> max_res = new ArrayList<>(); // 初始化结果数组
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
// 遇到M则开始找
if (students.get(i).get(j).equals("M")) { // 如果当前元素为M
getMaxConnected(students, i, j, max_res); // 在四个方向上搜索连续的M
}
}
}
Collections.sort(max_res); // 对结果数组排序
System.out.println(max_res.get(max_res.size() - 1)); // 输出最大的连续的M的个数
scanner.close();
}
}
import java.util.*;
public class Main {
// 定义四个方向的增量,分别表示:水平、垂直、对角线、反对角线
private static final int[][] DIRECTIONS = {{0, 1}, {1, 0}, {1, 1}, {-1, 1}};
public static void getMaxConnected(List<List<String>> students, int row, int column, List<Integer> res) {
int m = students.size(), n = students.get(0).size(); // 获取方阵的行数和列数
for (int[] dir : DIRECTIONS) { // 遍历每个方向
int len = 1; // 初始化连续的M的个数为1
int a = row, b = column; // 初始化起始位置
// 按当前方向搜索
while (a + dir[0] >= 0 && a + dir[0] < m && b + dir[1] >= 0 && b + dir[1] < n
&& students.get(a + dir[0]).get(b + dir[1]).equals("M")) {
a += dir[0]; // 更新行索引
b += dir[1]; // 更新列索引
len++; // 连续的M的个数加1
}
res.add(len); // 把连续的M的个数加入结果数组
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 读取矩阵大小
String[] dimensions = scanner.nextLine().split(",");
int row = Integer.parseInt(dimensions[0]);
int column = Integer.parseInt(dimensions[1]);
// 初始化方阵
List<List<String>> students = new ArrayList<>();
for (int i = 0; i < row; i++) {
String[] lineElements = scanner.nextLine().split(",");
students.add(Arrays.asList(lineElements));
}
List<Integer> max_res = new ArrayList<>(); // 初始化结果数组
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
// 遇到M则开始找
if (students.get(i).get(j).equals("M")) { // 如果当前元素为M
getMaxConnected(students, i, j, max_res); // 在四个方向上搜索连续的M
}
}
}
Collections.sort(max_res); // 对结果数组排序
System.out.println(max_res.get(max_res.size() - 1)); // 输出最大的连续的M的个数
scanner.close();
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129
Python
def get_max_connected(students, row, column, res):
length = 1 # 初始化连续的M的个数为1
a, b = 0, 0 # 初始化行和列的索引
m, n = len(students), len(students[0]) # 获取方阵的行数和列数
if column < n: # 从左往右搜索
a = row
b = column
while b < n - 1 and students[a][b + 1] == "M": # 不越界且下一个元素为M
b += 1
length += 1 # 连续的M的个数加1
res.append(length) # 把连续的M的个数加入结果数组
length = 1 # 重新初始化连续的M的个数为1
if row < m: # 从上往下搜索
a = row
b = column
while a < m - 1 and students[a + 1][b] == "M": # 不越界且下一个元素为M
a += 1
length += 1 # 连续的M的个数加1
res.append(length) # 把连续的M的个数加入结果数组
length = 1 # 重新初始化连续的M的个数为1
if row < m and column < n: # 对角线搜索
a = row
b = column
while a < m - 1 and b < n - 1 and students[a + 1][b + 1] == "M": # 不越界且下一个元素为M
a += 1
b += 1
length += 1 # 连续的M的个数加1
res.append(length) # 把连续的M的个数加入结果数组
length = 1 # 重新初始化连续的M的个数为1
if row >= 0 and column < n: # 从右往左搜索
a = row
b = column
while a > 0 and b < n - 1 and students[a - 1][b + 1] == "M": # 不越界且下一个元素为M
a -= 1
b += 1
length += 1 # 连续的M的个数加1
res.append(length) # 把连续的M的个数加入结果数组
if __name__ == "__main__":
input_str = input().strip()
row, column = map(int, input_str.split(","))
# 初始化方阵
students = []
for _ in range(row):
student_str = input().strip()
students.append(student_str.split(","))
max_res = [] # 初始化结果数组
for i in range(row):
for j in range(column):
if students[i][j] == "M":
get_max_connected(students, i, j, max_res) # 在四个方向上搜索连续的M
max_res.sort(reverse=True) # 对结果数组排序
print(max_res[0]) # 输出最大的连续的M的个数
import sys
# 定义四个方向的增量,分别表示:水平、垂直、对角线、反对角线
DIRECTIONS = [
(0, 1), (1, 0), (1, 1), (-1, 1)
]
def getMaxConnected(students, row, column, res):
m = len(students)
n = len(students[0])
for dir in DIRECTIONS:
len_m = 1 # 初始化连续的M的个数为1
a, b = row, column
# 按当前方向搜索
while (0 <= a + dir[0] < m) and (0 <= b + dir[1] < n) and students[a + dir[0]][b + dir[1]] == "M":
a += dir[0] # 更新行索引
b += dir[1] # 更新列索引
len_m += 1 # 连续的M的个数加1
res.append(len_m) # 把连续的M的个数加入结果数组
if __name__ == "__main__":
input_str = input().strip()
row, column = map(int, input_str.split(","))
# 初始化方阵
students = []
for _ in range(row):
student_str = input().strip()
students.append(student_str.split(","))
max_res = [] # 初始化结果数组
for i in range(row):
for j in range(column):
if students[i][j] == "M":
getMaxConnected(students, i, j, max_res) # 在四个方向上搜索连续的M
max_res.sort(reverse=True) # 对结果数组排序
print(max_res[0]) # 输出最大的连续的M的个数
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105
JavaScript
const readline = require('readline');
// 创建一个接口用于从标准输入输出流读取数据
const rl = readline.createInterface({
input: process.stdin, // 输入流为标准输入
output: process.stdout // 输出流为标准输出
});
// 定义一个函数,用于查找从某个点开始的最大连续的'M'数量
function getMaxConnected(students, row, column, res) {
let len = 1; // 初始化长度为1(至少包含自身)
let a = 0, b = 0; // a和b用于遍历学生方阵
const m = students.length, n = students[0].length; // 获取方阵的行数m和列数n
// 水平检查:从指定的列位置(column)向右遍历,直到非"M"或到达边界
if (column < n) {
a = row;
b = column;
while (b < n - 1 && students[a][++b] === "M") {
len++; // 如果找到"M",长度加1
}
res.push(len); // 将找到的长度添加到结果数组中
len = 1; // 重置长度为1,用于下一次方向检查
}
// 垂直检查:从指定的行位置(row)向下遍历,直到非"M"或到达边界
if (row < m) {
a = row;
b = column;
while (a < m - 1 && students[++a][b] === "M") {
len++; // 如果找到"M",长度加1
}
res.push(len); // 将找到的长度添加到结果数组中
len = 1; // 重置长度为1
}
// 对角线检查(左上到右下):从指定的位置向右下方遍历,直到非"M"或到达边界
if (row < m && column < n) {
a = row;
b = column;
while ((a < m - 1 && b < n - 1) && students[++a][++b] === "M") {
len++; // 如果找到"M",长度加1
}
res.push(len); // 将找到的长度添加到结果数组中
len = 1; // 重置长度为1
}
// 反对角线检查(左下到右上):从指定的位置向右上方遍历,直到非"M"或到达边界
if (row >= 0 && column < n) {
a = row;
b = column;
while ((a > 0 && b < n - 1) && students[--a][++b] === "M") {
len++; // 如果找到"M",长度加1
}
res.push(len); // 将找到的长度添加到结果数组中
}
}
// 监听标准输入的数据,当有输入时触发
rl.on('line', (input) => {
// 解析第一行输入,获取方阵的行数和列数
const [row, column] = input.split(",").map(Number);
const students = []; // 初始化一个二维数组用于存储学生数据
// 监听每一行的学生数据输入
rl.on('line', (student_str) => {
const temp = student_str.split(","); // 将输入按逗号分隔,得到一行学生数据
students.push(temp); // 将这一行数据加入students数组
// 当读取到的行数等于预期的行数时,开始处理数据
if (students.length === row) {
let max_res = []; // 初始化结果数组,用于存储每次搜索到的最大长度
// 遍历整个方阵
for (let i = 0; i < row; i++) {
for (let j = 0; j < column; j++) {
// 如果当前点是"M",则调用getMaxConnected函数查找
if (students[i][j] === "M") {
getMaxConnected(students, i, j, max_res);
}
}
}
// 对找到的所有长度排序,取最大值并输出
max_res.sort((a, b) => b - a);
console.log(max_res[0]);
rl.close(); // 关闭读取接口
}
});
});
const readline = require('readline');
// 创建接口以读取输入
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
// 定义四个方向的增量,分别表示:水平、垂直、对角线、反对角线
const DIRECTIONS = [
[0, 1], [1, 0], [1, 1], [-1, 1]
];
function getMaxConnected(students, row, column, res) {
const m = students.length;
const n = students[0].length;
for (const dir of DIRECTIONS) {
let len = 1; // 初始化连续的M的个数为1
let a = row, b = column;
// 按当前方向搜索
while (a + dir[0] >= 0 && a + dir[0] < m && b + dir[1] >= 0 && b + dir[1] < n
&& students[a + dir[0]][b + dir[1]] === "M") {
a += dir[0]; // 更新行索引
b += dir[1]; // 更新列索引
len++; // 连续的M的个数加1
}
res.push(len); // 把连续的M的个数加入结果数组
}
}
rl.on('line', (input) => {
const [row, column] = input.split(",").map(Number);
const students = [];
rl.on('line', (student_str) => {
const temp = student_str.split(",");
students.push(temp);
if (students.length === row) {
let max_res = [];
for (let i = 0; i < row; i++) {
for (let j = 0; j < column; j++) {
if (students[i][j] === "M") {
getMaxConnected(students, i, j, max_res);
}
}
}
max_res.sort((a, b) => b - a);
console.log(max_res[0]);
rl.close();
}
});
});
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148
C++
#include <iostream>
#include <vector>
#include <string>
#include <sstream>
#include <algorithm>
using namespace std;
void getMaxConnected(vector<vector<string>>& students, int row, int column, vector<int>& res) {
int len = 1; // 初始化连续的M的个数为1
int a = 0, b = 0; // 初始化行和列的索引
int m = students.size(), n = students[0].size(); // 获取方阵的行数和列数
if (column < n) { // 从左往右搜索
a = row;
b = column;
while (b < n - 1 && students[a][++b] == "M") { // 不越界且下一个元素为M
len++; // 连续的M的个数加1
}
res.push_back(len); // 把连续的M的个数加入结果数组
len = 1; // 重新初始化连续的M的个数为1
}
if (row < m) { // 从上往下搜索
a = row;
b = column;
while (a < m - 1 && students[++a][b] == "M") { // 不越界且下一个元素为M
len++; // 连续的M的个数加1
}
res.push_back(len); // 把连续的M的个数加入结果数组
len = 1; // 重新初始化连续的M的个数为1
}
if (row < m && column < n) { // 对角线搜索
a = row;
b = column;
while ((a < m - 1 && b < n - 1) && students[++a][++b] == "M") { // 不越界且下一个元素为M
len++; // 连续的M的个数加1
}
res.push_back(len); // 把连续的M的个数加入结果数组
len = 1; // 重新初始化连续的M的个数为1
}
if (row >= 0 && column < n) { // 从右往左搜索
a = row;
b = column;
while ((a > 0 && b < n - 1) && students[--a][++b] == "M") { // 不越界且下一个元素为M
len++; // 连续的M的个数加1
}
res.push_back(len); // 把连续的M的个数加入结果数组
}
}
int main() {
string input_str;
getline(cin, input_str);
// 解析行数和列数
stringstream ss(input_str);
string temp;
getline(ss, temp, ',');
int row = stoi(temp);
getline(ss, temp);
int column = stoi(temp);
// 初始化方阵
vector<vector<string>> students(row, vector<string>(column));
for (int i = 0; i < row; ++i) {
getline(cin, input_str);
stringstream ss(input_str);
for (int j = 0; j < column; ++j) {
getline(ss, students[i][j], ',');
}
}
vector<int> max_res; // 初始化结果数组
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
//遇到M则开始找
if (students[i][j] == "M") { // 如果当前元素为M
getMaxConnected(students, i, j, max_res); // 在四个方向上搜索连续的M
}
}
}
sort(max_res.begin(), max_res.end()); // 对结果数组排序
cout << max_res[max_res.size()-1]; // 输出最大的连续的M的个数
return 0;
}
#include <iostream>
#include <vector>
#include <string>
#include <sstream>
#include <algorithm>
using namespace std;
// 定义四个方向的增量,分别表示:水平、垂直、对角线、反对角线
const vector<vector<int>> DIRECTIONS = {{0, 1}, {1, 0}, {1, 1}, {-1, 1}};
void getMaxConnected(const vector<vector<string>>& students, int row, int column, vector<int>& res) {
int m = students.size();
int n = students[0].size();
for (const auto& dir : DIRECTIONS) {
int len = 1; // 初始化连续的M的个数为1
int a = row, b = column;
// 按当前方向搜索
while (a + dir[0] >= 0 && a + dir[0] < m && b + dir[1] >= 0 && b + dir[1] < n
&& students[a + dir[0]][b + dir[1]] == "M") {
a += dir[0]; // 更新行索引
b += dir[1]; // 更新列索引
len++; // 连续的M的个数加1
}
res.push_back(len); // 把连续的M的个数加入结果数组
}
}
int main() {
string input_str;
getline(cin, input_str);
// 解析行数和列数
stringstream ss(input_str);
string temp;
getline(ss, temp, ',');
int row = stoi(temp);
getline(ss, temp);
int column = stoi(temp);
// 初始化方阵
vector<vector<string>> students(row, vector<string>(column));
for (int i = 0; i < row; ++i) {
getline(cin, input_str);
stringstream ss(input_str);
for (int j = 0; j < column; ++j) {
getline(ss, students[i][j], ',');
}
}
vector<int> max_res; // 初始化结果数组
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
if (students[i][j] == "M") {
getMaxConnected(students, i, j, max_res); // 在四个方向上搜索连续的M
}
}
}
sort(max_res.begin(), max_res.end(), greater<int>()); // 对结果数组排序
cout << max_res[0] << endl; // 输出最大的连续的M的个数
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155
C语言
#include <stdio.h>
#include <stdlib.h>
int main() {
int n, m; // 定义矩阵的行数和列数
scanf("%d,%d\n", &n, &m); // 读取矩阵的行数和列数
char students[n][m]; // 定义字符矩阵以存储输入
for (int i = 0; i < n; i++) { // 遍历每一行
for (int j = 0; j < m; j++) { // 遍历每一列
scanf("%c", &students[i][j]); // 读取字符并存入矩阵
getchar(); // 吃掉换行符或逗号
}
}
int max_res[n * m]; // 用于存储每次搜索到的连续M的个数
int res_size = 0; // 记录结果数组的实际大小
// 遍历整个矩阵,查找连续的M
for (int i = 0; i < n; i++) { // 遍历行
for (int j = 0; j < m; j++) { // 遍历列
if (students[i][j] == 'M') { // 如果当前字符是'M'
int len = 1; // 初始化连续M的长度为1
int a = 0, b = 0; // 初始化行和列索引
// 从左往右搜索
if (j < m) {
a = i;
b = j;
while (b < m - 1 && students[a][++b] == 'M') { // 不越界且下一个元素为M
len++; // 连续的M的个数加1
}
max_res[res_size++] = len; // 把找到的连续M的个数存入结果数组
len = 1; // 重置长度为1
}
// 从上往下搜索
if (i < n) {
a = i;
b = j;
while (a < n - 1 && students[++a][b] == 'M') { // 不越界且下一个元素为M
len++; // 连续的M的个数加1
}
max_res[res_size++] = len; // 把找到的连续M的个数存入结果数组
len = 1; // 重置长度为1
}
// 对角线搜索(左上到右下)
if (i < n && j < m) {
a = i;
b = j;
while (a < n - 1 && b < m - 1 && students[++a][++b] == 'M') { // 不越界且下一个元素为M
len++; // 连续的M的个数加1
}
max_res[res_size++] = len; // 把找到的连续M的个数存入结果数组
len = 1; // 重置长度为1
}
// 对角线搜索(左下到右上)
if (i >= 0 && j < m) {
a = i;
b = j;
while (a > 0 && b < m - 1 && students[--a][++b] == 'M') { // 不越界且下一个元素为M
len++; // 连续的M的个数加1
}
max_res[res_size++] = len; // 把找到的连续M的个数存入结果数组
}
}
}
}
// 对结果数组进行排序,找到最大的连续M的个数
int max = max_res[0];
for (int i = 1; i < res_size; i++) {
if (max_res[i] > max) {
max = max_res[i];
}
}
// 输出最大的连续M的个数
printf("%d\n", max);
return 0;
}
#include <stdio.h>
#include <stdlib.h>
// 定义四个方向的增量,分别表示:水平、垂直、对角线、反对角线
const int DIRECTIONS[4][2] = {{0, 1}, {1, 0}, {1, 1}, {-1, 1}};
int main() {
int n, m; // 定义矩阵的行数和列数
scanf("%d,%d\n", &n, &m); // 读取矩阵的行数和列数
char students[n][m]; // 定义字符矩阵以存储输入
for (int i = 0; i < n; i++) { // 遍历每一行
for (int j = 0; j < m; j++) { // 遍历每一列
scanf("%c", &students[i][j]); // 读取字符并存入矩阵
getchar(); // 吃掉换行符或逗号
}
}
int max_res[n * m]; // 用于存储每次搜索到的连续M的个数
int res_size = 0; // 记录结果数组的实际大小
// 遍历整个矩阵,查找连续的M
for (int i = 0; i < n; i++) { // 遍历行
for (int j = 0; j < m; j++) { // 遍历列
if (students[i][j] == 'M') { // 如果当前字符是'M'
// 在四个方向上搜索
for (int d = 0; d < 4; d++) {
int len = 1; // 初始化连续M的长度为1
int a = i, b = j; // 初始化当前的位置
// 按当前方向搜索连续的M
while (a + DIRECTIONS[d][0] >= 0 && a + DIRECTIONS[d][0] < n &&
b + DIRECTIONS[d][1] >= 0 && b + DIRECTIONS[d][1] < m &&
students[a + DIRECTIONS[d][0]][b + DIRECTIONS[d][1]] == 'M') {
a += DIRECTIONS[d][0]; // 更新行索引
b += DIRECTIONS[d][1]; // 更新列索引
len++; // 连续的M的个数加1
}
max_res[res_size++] = len; // 把找到的连续M的个数存入结果数组
}
}
}
}
// 对结果数组进行排序,找到最大的连续M的个数
int max = max_res[0];
for (int i = 1; i < res_size; i++) {
if (max_res[i] > max) {
max = max_res[i];
}
}
// 输出最大的连续M的个数
printf("%d\n", max);
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145
三维数据解法
Java
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 读取矩阵大小
String[] dimensions = scanner.nextLine().split(",");
int row = Integer.parseInt(dimensions[0]);
int column = Integer.parseInt(dimensions[1]);
// 初始化方阵
List<List<String>> students = new ArrayList<>();
for (int i = 0; i < row; i++) {
String[] lineElements = scanner.nextLine().split(",");
students.add(Arrays.asList(lineElements));
}
int max_res = 0;
int[][][] dp = new int[row + 2][column + 2][4];
for (int i = 1; i <= row; i++) {
for (int j = 1; j <= column; j++) {
if (students.get(i - 1).get(j - 1).equals("M")) {
dp[i][j][0] = dp[i - 1][j][0] + 1;
dp[i][j][1] = dp[i][j - 1][1] + 1;
dp[i][j][2] = dp[i - 1][j - 1][2] + 1;
dp[i][j][3] = dp[i - 1][j + 1][3] + 1;
max_res = Math.max(max_res, Math.max(Math.max(dp[i][j][0], dp[i][j][1]), Math.max(dp[i][j][2], dp[i][j][3])));
}
}
}
System.out.println(max_res);
}
}
1234567891011121314151617181920212223242526272829303132333435363738
Python
# 读入矩阵的行数和列数
m , n = map(int, input().split(','))
# 读入矩阵元素,将'M'转换为1,其余转换为0
M = []
for i in range(m):
M.append([1 if i == 'M' else 0 for i in input().split(',')])
# 初始化dp数组,dp[i][j]表示从该点开始向上、向左、向左上、向右上四个方向最多能连续多少个1
dp = [[[0] * 4 for _ in range(n + 2)] for _ in range(m + 2)]
ans = 0
# 遍历矩阵
for i in range(1, m + 1):
for j in range(1, n + 1):
# 如果该点为1
if M[i - 1][j - 1] == 1:
# 更新向上、向左、向左上、向右上四个方向的最大连续1的个数
dp[i][j][0] = dp[i - 1][j][0] + 1
dp[i][j][1] = dp[i][j - 1][1] + 1
dp[i][j][2] = dp[i - 1][j - 1][2] + 1
dp[i][j][3] = dp[i - 1][j + 1][3] + 1
# 更新最大连续1的个数
ans = max(ans, max(dp[i][j]))
# 输出最大连续1的个数
print(ans)
1234567891011121314151617181920212223242526
JavaScript
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let students = [];
let row, column;
rl.on('line', (input) => {
if (!row) {
// 解析第一行输入,获取方阵的行数和列数
[row, column] = input.split(",").map(Number);
} else {
const temp = input.split(","); // 将输入按逗号分隔,得到一行学生数据
students.push(temp); // 将这一行数据加入students数组
// 当读取到的行数等于预期的行数时,开始处理数据
if (students.length === row) {
let max_res = 0;
let dp = Array(row + 2).fill(null).map(() => Array(column + 2).fill(null).map(() => Array(4).fill(0)));
for (let i = 1; i <= row; i++) {
for (let j = 1; j <= column; j++) {
if (students[i - 1][j - 1] === "M") {
dp[i][j][0] = dp[i - 1][j][0] + 1;
dp[i][j][1] = dp[i][j - 1][1] + 1;
dp[i][j][2] = dp[i - 1][j - 1][2] + 1;
dp[i][j][3] = dp[i - 1][j + 1][3] + 1;
max_res = Math.max(max_res, Math.max(dp[i][j][0], dp[i][j][1], dp[i][j][2], dp[i][j][3]));
}
}
}
console.log(max_res);
rl.close(); // 关闭读取接口
}
}
});
12345678910111213141516171819202122232425262728293031323334353637383940
C++
#include <iostream>
#include <sstream>
#include <vector>
#include <algorithm>
using namespace std;
int main() {
string input_str;
getline(cin, input_str);
// 解析行数和列数
stringstream ss(input_str);
string temp;
getline(ss, temp, ',');
int row = stoi(temp);
getline(ss, temp);
int column = stoi(temp);
// 初始化方阵
vector<vector<string>> students(row, vector<string>(column));
for (int i = 0; i < row; ++i) {
getline(cin, input_str);
stringstream ss(input_str);
for (int j = 0; j < column; ++j) {
getline(ss, students[i][j], ',');
}
}
int max_res = 0;
vector<vector<vector<int>>> dp(row + 2, vector<vector<int>>(column + 2, vector<int>(4, 0)));
for (int i = 1; i <= row; ++i) {
for (int j = 1; j <= column; ++j) {
if (students[i - 1][j - 1] == "M") {
dp[i][j][0] = dp[i - 1][j][0] + 1;
dp[i][j][1] = dp[i][j - 1][1] + 1;
dp[i][j][2] = dp[i - 1][j - 1][2] + 1;
dp[i][j][3] = dp[i - 1][j + 1][3] + 1;
max_res = max(max_res, max({dp[i][j][0], dp[i][j][1], dp[i][j][2], dp[i][j][3]}));
}
}
}
cout << max_res << endl;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748
C语言
#include <stdio.h>
int main() {
int n, m; // 定义矩阵的行数和列数
scanf("%d,%d\n", &n, &m); // 读取矩阵的行数和列数
char students[n][m]; // 定义字符矩阵以存储输入
for (int i = 0; i < n; i++) { // 遍历每一行
for (int j = 0; j < m; j++) { // 遍历每一列
scanf("%c", &students[i][j]); // 读取字符并存入矩阵
getchar(); // 吃掉换行符或逗号
}
}
int dp[n + 2][m + 2][4]; // 初始化dp数组
for (int i = 0; i < n + 2; i++) {
for (int j = 0; j < m + 2; j++) {
for (int k = 0; k < 4; k++) {
dp[i][j][k] = 0;
}
}
}
int max_res = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (students[i - 1][j - 1] == 'M') {
dp[i][j][0] = dp[i - 1][j][0] + 1; // 向上方向
dp[i][j][1] = dp[i][j - 1][1] + 1; // 向左方向
dp[i][j][2] = dp[i - 1][j - 1][2] + 1; // 左上方向
dp[i][j][3] = dp[i - 1][j + 1][3] + 1; // 右上方向
int local_max = dp[i][j][0];
for (int k = 1; k < 4; k++) {
if (dp[i][j][k] > local_max) {
local_max = dp[i][j][k];
}
}
if (local_max > max_res) {
max_res = local_max;
}
}
}
}
printf("%d\n", max_res); // 输出最大连续1的个数
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950
大厂原题(全网最全,持续更新) 文章被收录于专栏
主要记录自己的刷题日常,学而时习之。