E卷100分题 - 机器人活动区域
题目描述
现有一个机器人,可放置于 M × N 的网格中任意位置,每个网格包含一个非负整数编号,当相邻网格的数字编号差值的绝对值小于等于 1 时,机器人可以在网格间移动。
问题: 求机器人可活动的最大范围对应的网格点数目。
说明:网格左上角坐标为 (0,0) ,右下角坐标为(m−1,n−1),机器人只能在相邻网格间上下左右移动
输入描述
第 1 行输入为 M 和 N
- M 表示网格的行数
- N 表示网格的列数
之后 M 行表示网格数值,每行 N 个数值(数值大小用 k 表示),数值间用单个空格分隔,行首行尾无多余空格。
- M、 N、 k 均为整数
- 1 ≤ M,N ≤ 150,
- 0 ≤ k ≤ 50
输出描述
输出 1 行,包含 1 个数字,表示最大活动区域的网格点数目,
行首行尾无多余空格。
示例1
输入
4 4
1 2 5 2
2 4 4 5
3 5 7 1
4 6 2 4
12345
输出
6
1
说明
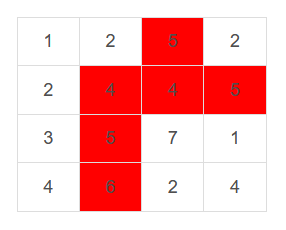
如下图: 图中红色区域,相邻网格差值绝对值都小于等于 1 ,且为最大区域,对应网格点数目为 6。
示例2
输入
2 3
1 3 5
4 1 3
123
输出
1
1
说明
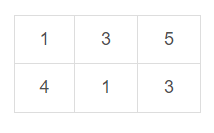
任意两个相邻网格的差值绝对值都大于1,机器人不能在网格间移动,只能在单个网格内活动,对应网格点数目为1
解题思路
使用BFS求最大连通分量,规则:当相邻网格的数字编号差值的绝对值小于等于 1 时
Java
import java.util.Scanner;
class Main {
// 定义四个方向,上下左右
private static final int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public static void main(String[] args) {
// 输入处理
Scanner in = new Scanner(System.in);
int m = in.nextInt(); // 行数
int n = in.nextInt(); // 列数
int[][] matrix = new int[m][n]; // 定义矩阵
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
matrix[i][j] = in.nextInt(); // 读入矩阵中的值
}
}
// 遍历每个点作为起点,求最大活动范围
int maxRange = 0; // 定义最大活动范围
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
boolean[][] visited = new boolean[m][n]; // 定义是否访问过
int range = dfs(matrix, visited, i, j); // 深度优先搜索
maxRange = Math.max(maxRange, range); // 更新最大活动范围
}
}
System.out.println(maxRange); // 输出最大活动范围
}
public static int dfs(int[][] matrix, boolean[][] visited, int x, int y) {
visited[x][y] = true; // 标记当前点已经访问过
int range = 1; // 定义活动范围
for (int[] direction : directions) { // 遍历四个方向
int newX = x + direction[0]; // 新的横坐标
int newY = y + direction[1]; // 新的纵坐标
if (newX >= 0 && newX < matrix.length && newY >= 0 && newY < matrix[0].length
&& !visited[newX][newY] && Math.abs(matrix[newX][newY] - matrix[x][y]) <= 1) { // 判断是否越界、是否访问过、是否符合条件
range += dfs(matrix, visited, newX, newY); // 更新活动范围
}
}
return range; // 返回活动范围
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546
Python
import sys
# 定义四个可能的移动方向:右,左,下,上
directions = [[0, 1], [0, -1], [1, 0], [-1, 0]]
# 使用深度优先搜索(DFS)来探索网格
def dfs(matrix, visited, x, y):
# 标记当前网格点为已访问
visited[x][y] = True
# 初始化当前网格点的范围计数为1
range = 1
# 遍历所有可能的移动方向
for direction in directions:
newX = x + direction[0] # 计算新的行坐标
newY = y + direction[1] # 计算新的列坐标
# 检查新坐标是否在网格内部,且未访问过,并且满足编号差值绝对值小于等于1的条件
if newX >= 0 and newX < len(matrix) and newY >= 0 and newY < len(matrix[0]) \
and not visited[newX][newY] and abs(matrix[newX][newY] - matrix[x][y]) <= 1:
# 递归地继续探索并累加可活动的网格点数目
range += dfs(matrix, visited, newX, newY)
# 返回从当前网格点出发可活动的最大网格点数目
return range
# 读取输入数据
m, n = 0, 0 # 初始化网格的行数和列数
matrix = [] # 初始化网格矩阵
# 逐行读取输入
for line in sys.stdin:
if not m and not n:
m, n = map(int, line.split()) # 读取网格的行数和列数
else:
matrix.append(list(map(int, line.split()))) # 读取网格中的数值
if len(matrix) == m: # 如果已经读取完所有行,结束读取
break
# 寻找机器人可以活动的最大范围
maxRange = 0
for i in range(m):
for j in range(n):
visited = [[False] * n for _ in range(m)] # 初始化访问标记数组
ranges = dfs(matrix, visited, i, j) # 对每个网格点执行DFS
maxRange = max(maxRange, ranges) # 更新最大活动范围
# 输出机器人可以活动的最大范围对应的网格点数目
print(maxRange)
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647
JavaScript
// 导入readline模块以读取和处理输入数据
const readline = require('readline');
// 创建readline接口,配置输入来自标准输入,输出到标准输出
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
// 定义四个可能的移动方向:右,左,下,上
const directions = [[0, 1], [0, -1], [1, 0], [-1, 0]];
// 使用深度优先搜索(DFS)来探索网格
function dfs(matrix, visited, x, y) {
visited[x][y] = true; // 标记当前网格点为已访问
let range = 1; // 初始化当前网格点的范围计数为1
// 遍历所有可能的移动方向
for (let direction of directions) {
let newX = x + direction[0]; // 计算新的行坐标
let newY = y + direction[1]; // 计算新的列坐标
// 检查新坐标是否在网格内部,且未访问过,并且满足编号差值绝对值小于等于1的条件
if (newX >= 0 && newX < matrix.length && newY >= 0 && newY < matrix[0].length
&& !visited[newX][newY] && Math.abs(matrix[newX][newY] - matrix[x][y]) <= 1) {
range += dfs(matrix, visited, newX, newY); // 递归地继续探索并累加可活动的网格点数目
}
}
return range; // 返回从当前网格点出发可活动的最大网格点数目
}
let m, n; // 声明变量m和n来存储网格的行数和列数
let matrix = []; // 初始化网格矩阵
// 处理每行输入
rl.on('line', (line) => {
if (!m && !n) {
[m, n] = line.split(' ').map(Number); // 解析输入的行数和列数
return;
}
matrix.push(line.split(' ').map(Number)); // 读取网格中的数值
if (matrix.length === m) { // 如果已经读取完所有行,关闭输入流
rl.close();
}
});
// 输入流关闭后开始处理数据
rl.on('close', () => {
let maxRange = 0; // 初始化最大活动范围
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
let visited = Array.from({length: m}, () => Array(n).fill(false)); // 初始化访问标记数组
let range = dfs(matrix, visited, i, j); // 对每个网格点执行DFS
maxRange = Math.max(maxRange, range); // 更新最大活动范围
}
}
console.log(maxRange); // 输出机器人可以活动的最大范围对应的网格点数目
});
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657
C++
#include <iostream>
#include <vector>
using namespace std;
// 定义四个方向,上下左右
const vector<vector<int>> directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
int dfs(vector<vector<int>>& matrix, vector<vector<bool>>& visited, int x, int y) {
visited[x][y] = true; // 标记当前点已经访问过
int range = 1; // 定义活动范围
for (vector<int> direction : directions) { // 遍历四个方向
int newX = x + direction[0]; // 新的横坐标
int newY = y + direction[1]; // 新的纵坐标
if (newX >= 0 && newX < matrix.size() && newY >= 0 && newY < matrix[0].size()
&& !visited[newX][newY] && abs(matrix[newX][newY] - matrix[x][y]) <= 1) { // 判断是否越界、是否访问过、是否符合条件
range += dfs(matrix, visited, newX, newY); // 更新活动范围
}
}
return range; // 返回活动范围
}
int main() {
// 输入处理
int m, n;
cin >> m >> n;
vector<vector<int>> matrix(m, vector<int>(n)); // 定义矩阵
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> matrix[i][j]; // 读入矩阵中的值
}
}
// 遍历每个点作为起点,求最大活动范围
int maxRange = 0; // 定义最大活动范围
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
vector<vector<bool>> visited(m, vector<bool>(n, false)); // 定义是否访问过
int range = dfs(matrix, visited, i, j); // 深度优先搜索
maxRange = max(maxRange, range); // 更新最大活动范围
}
}
cout << maxRange << endl; // 输出最大活动范围
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647
C语言
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
// 定义四个方向,上下左右
int directions[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
// 深度优先搜索函数
int dfs(int **matrix, bool **visited, int x, int y, int m, int n) {
visited[x][y] = true; // 标记当前点已经访问过
int range = 1; // 定义活动范围
for (int i = 0; i < 4; i++) { // 遍历四个方向
int newX = x + directions[i][0]; // 新的横坐标
int newY = y + directions[i][1]; // 新的纵坐标
// 判断是否越界、是否访问过、是否符合条件
if (newX >= 0 && newX < m && newY >= 0 && newY < n &&
!visited[newX][newY] && abs(matrix[newX][newY] - matrix[x][y]) <= 1) {
range += dfs(matrix, visited, newX, newY, m, n); // 更新活动范围
}
}
return range; // 返回活动范围
}
int main() {
int m, n;
scanf("%d %d", &m, &n); // 输入行数和列数
// 动态分配矩阵空间
int **matrix = (int **)malloc(m * sizeof(int *));
for (int i = 0; i < m; i++) {
matrix[i] = (int *)malloc(n * sizeof(int));
}
// 动态分配访问标记数组空间
bool **visited = (bool **)malloc(m * sizeof(bool *));
for (int i = 0; i < m; i++) {
visited[i] = (bool *)malloc(n * sizeof(bool));
}
// 读入矩阵中的值
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
scanf("%d", &matrix[i][j]);
}
}
int maxRange = 0; // 定义最大活动范围
// 遍历每个点作为起点,求最大活动范围
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// 初始化访问标记数组为未访问
for (int a = 0; a < m; a++) {
for (int b = 0; b < n; b++) {
visited[a][b] = false;
}
}
int range = dfs(matrix, visited, i, j, m, n); // 深度优先搜索
if (range > maxRange) {
maxRange = range; // 更新最大活动范围
}
}
}
printf("%d\n", maxRange); // 输出最大活动范围
// 释放分配的内存
for (int i = 0; i < m; i++) {
free(matrix[i]);
free(visited[i]);
}
free(matrix);
free(visited);
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576
大厂原题(全网最全,持续更新) 文章被收录于专栏
主要记录自己的刷题日常,学而时习之。
 查看5道真题和解析
查看5道真题和解析