2022春招,必须拿捏的十道算法题
前言
大家好,我是bigsai。
最近不少小伙伴跟我交流刷题肿么刷,我给的建议就是先剑指offer和力扣hot100,在这些题中还有些重要程度和出现频率是非常非常高的,今天给大家分享当今出现频率最高的10道算法题,学到就是赚到。
0X01翻转链表
力扣206和剑指offer24原题,题意为:
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
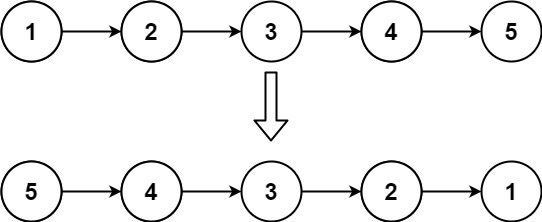
分析:
翻转链表,本意是不创建新的链表节点然后在原链表上实现翻转,但是这个图有点会误导人的思维,其实更好的理解你可以看下面这幅图:
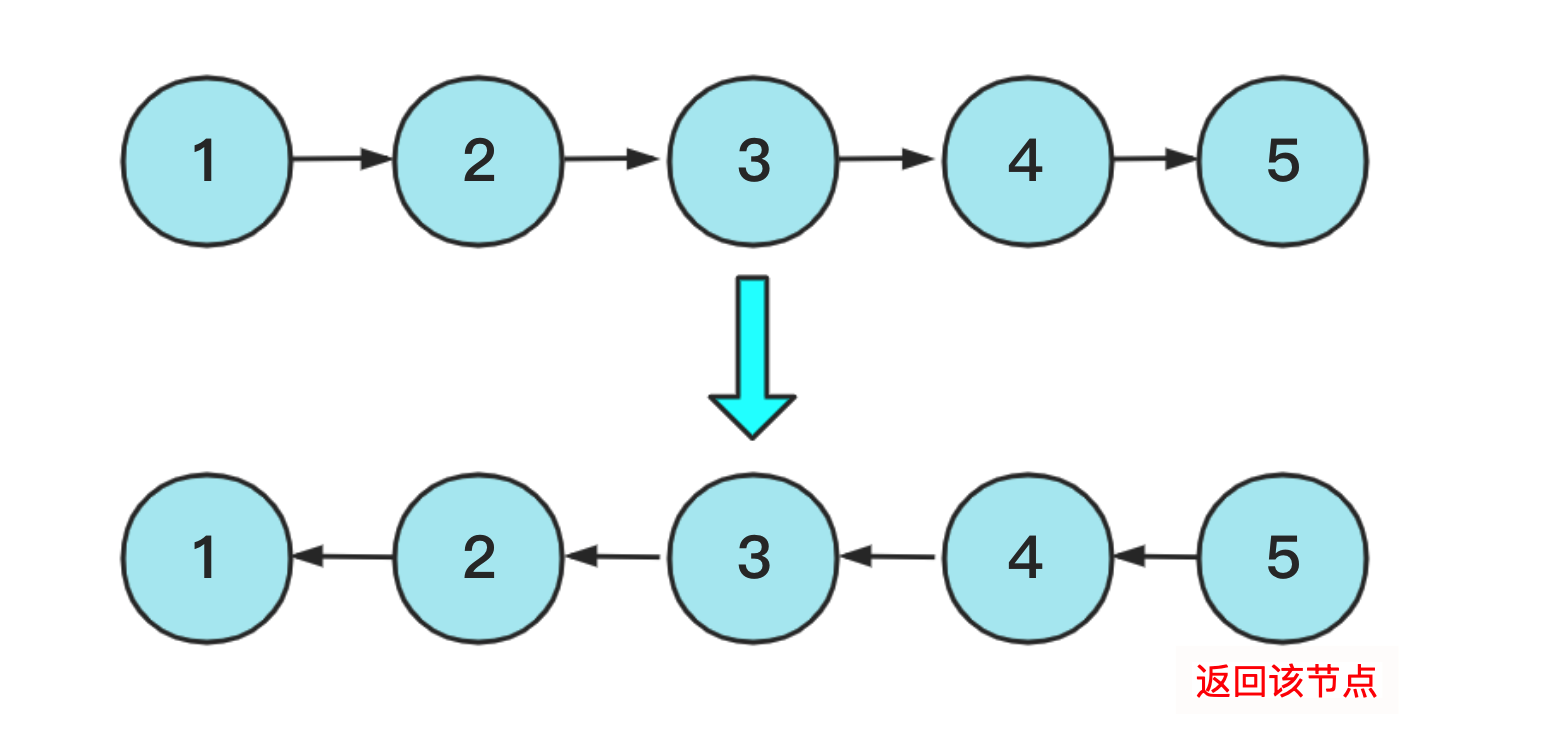
具体实现上两个思路,非递归和递归的实现方式,非递归的实现方式比较简单,利用一个pre节点记录前驱节点,向下枚举的时候改变指针指向就可以,实现代码为:
class Solution {
public ListNode reverseList(ListNode head) {
if(head==null||head.next==null)//如果节点为NULL或者单个节点直接返回
return head;
ListNode pre=head;//前驱节点
ListNode cur=head.next;//当前节点用来枚举
while (cur!=null)
{
ListNode next=cur.next;
//改变指向
cur.next=pre;
pre=cur;
cur=next;
}
head.next=null;//将原先的head节点next置null防止最后成环
return pre;
}
} 而递归的方式比较巧妙,借助递归归来的过程巧妙改变指针指向和返回值传递,代码虽然精简但是理解起来有一定难度的,这里用一张图帮助大家理解:
具体代码为:
class Solution {
public ListNode reverseList(ListNode head) {
if(head==null||head.next==null)//如果最后一个节点不操作
return head;
ListNode node =reverseList(head.next);//先递归 到最底层 然后返回
head.next.next=head;//后面一个节点指向自己
head.next=null;//自己本来指向的next置为null
return node;//返回最后一个节点(一直被递归传递)
}
} 0X02设计LRU
对应力扣146LRU缓存机制,题目要求为:
运用你所掌握的数据结构,设计和实现一个 LRU 缓存机制 。实现 LRUCache 类:
LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
void put(int key, int value) 如果关键字已经存在,则变更其数据值;如果关键字不存在,则插入该组「关键字-值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
进阶:在 O(1) 时间复杂度内完成这两种操作
详细分析:
LRU的核心就是借助哈希+双链表,哈希用于查询,双链表实现删除只知道当前节点也能O(1)的复杂度删除,不过双链表需要考虑的头尾指针特殊情况。
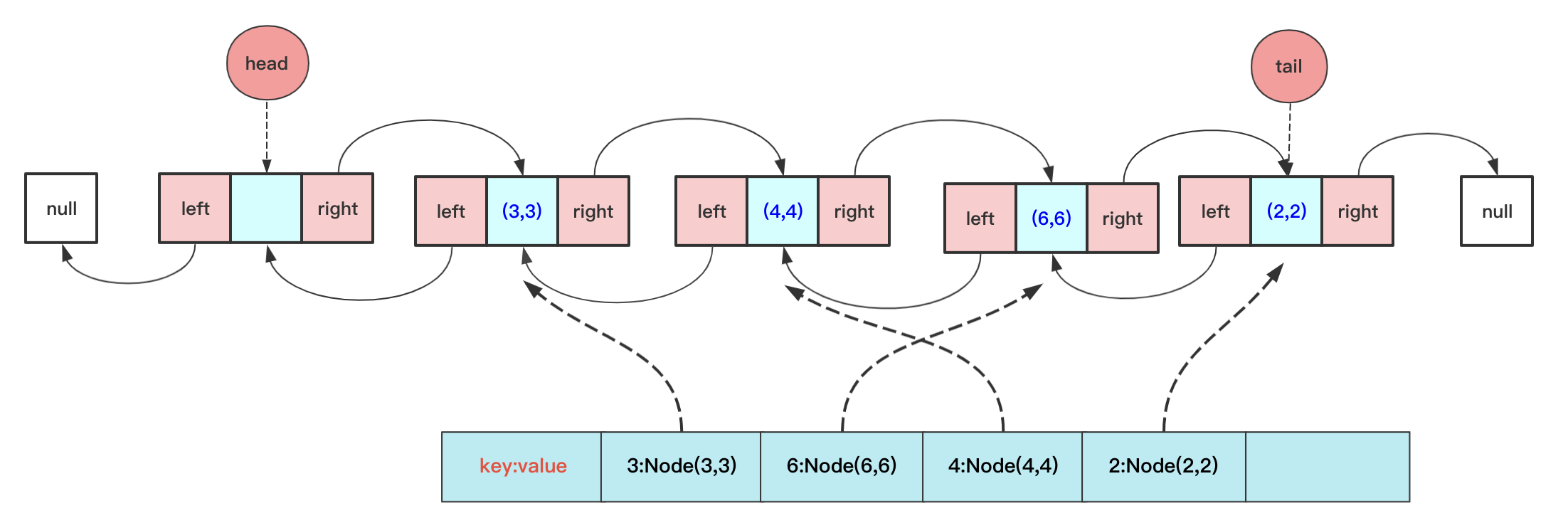
具体实现的代码为:
class LRUCache {
class Node {
int key;
int value;
Node pre;
Node next;
public Node() {
}
public Node( int key,int value) {
this.key = key;
this.value=value;
}
}
class DoubleList{
private Node head;// 头节点
private Node tail;// 尾节点
private int length;
public DoubleList() {
head = new Node(-1,-1);
tail = head;
length = 0;
}
void add(Node teamNode)// 默认尾节点插入
{
tail.next = teamNode;
teamNode.pre=tail;
tail = teamNode;
length++;
}
void deleteFirst(){
if(head.next==null)
return;
if(head.next==tail)//如果删除的那个刚好是tail 注意啦 tail指针前面移动
tail=head;
head.next=head.next.next;
if(head.next!=null)
head.next.pre=head;
length--;
}
void deleteNode(Node team){
team.pre.next=team.next;
if(team.next!=null)
team.next.pre=team.pre;
if(team==tail)
tail=tail.pre;
team.pre=null;
team.next=null;
length--;
}
}
Map<Integer,Node> map=new HashMap<>();
DoubleList doubleList;//存储顺序
int maxSize;
LinkedList<Integer>list2=new LinkedList<>();
public LRUCache(int capacity) {
doubleList=new DoubleList();
maxSize=capacity;
}
public int get(int key) {
int val;
if(!map.containsKey(key))
return -1;
val=map.get(key).value;
Node team=map.get(key);
doubleList.deleteNode(team);
doubleList.add(team);
return val;
}
public void put(int key, int value) {
if(map.containsKey(key)){// 已经有这个key 不考虑长短直接删除然后更新
Node deleteNode=map.get(key);
doubleList.deleteNode(deleteNode);
}
else if(doubleList.length==maxSize){//不包含并且长度小于
Node first=doubleList.head.next;
map.remove(first.key);
doubleList.deleteFirst();
}
Node node=new Node(key,value);
doubleList.add(node);
map.put(key,node);
}
} 0X03环形链表
对应力扣141和力扣142,力扣141环形链表要求为:
给定一个链表,判断链表中是否有环,用O(1)内存解决。
详细分析:
这个问题利用快慢双指针比较高效,快指针fast每次走2步,slow每次走1步,慢指针走n步到尾时候快指针走了2n步,而环的大小一定小于等于n所以一定会相遇,如果相遇那么说明有环,如果不相遇fast先为null说明无环。
具体代码为:
public class Solution {
public boolean hasCycle(ListNode head) {
ListNode fast=head;
ListNode slow=fast;
while (fast!=null&&fast.next!=null) {
slow=slow.next;
fast=fast.next.next;
if(fast==slow)
return true;
}
return false;
}
} 力扣142是在力扣141拓展,如有有环,返回入环的那个节点,就想下图环形链表返回节点2。

这个问题是需要数学转换的,具体的分析可以看上面的详细分析,这里面提一下大题的步骤。
如果找到第一个交汇点,其中一个停止,另一个继续走,下一次交汇时候刚好走一圈,可以算出循环部分长度为y。
所以我们知道的东西有:交汇时候fast走2x步,slow走x步,环长为y。并且快指针和慢指针交汇时候,多走的步数刚好是换长y的整数倍(它两此刻在同一个位置,快指针刚好多绕整数倍圈数才能在同一个位置相聚),可以得到2x=x+ny(x=ny)。其中所以说慢指针走的x和快指针多走的x是圈长y的整数倍。
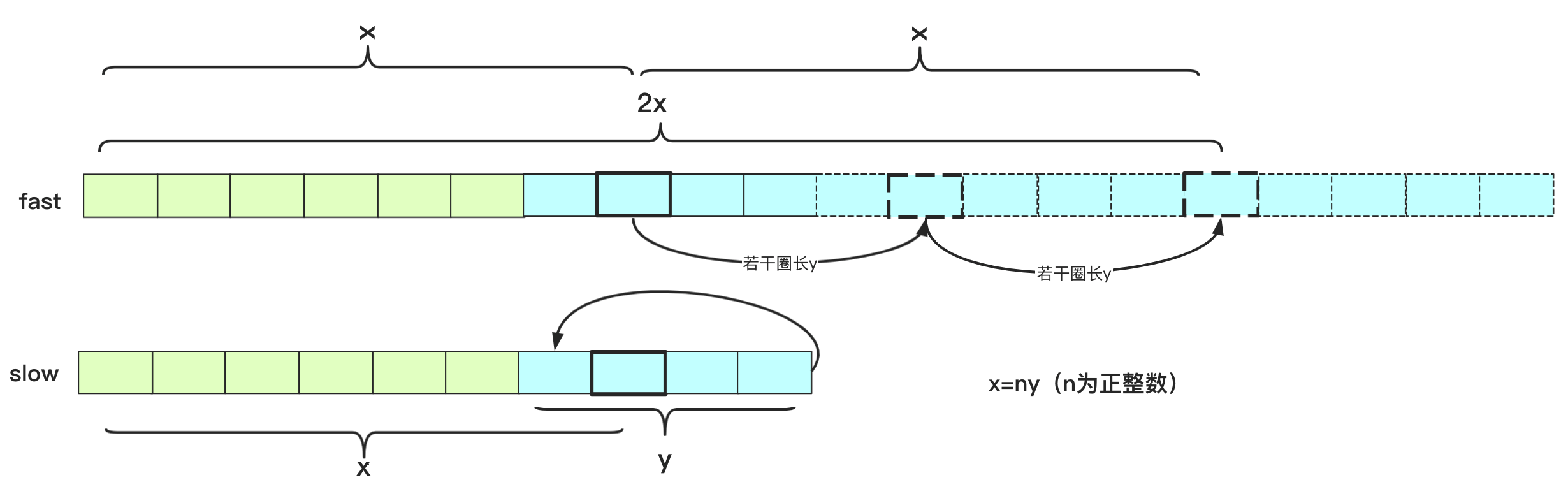
也就是说,从开头走到这个点共计x步,从这个点走x步也就是绕了几圈也回到这个点。如果说slow从起点出发,fast从这个点出发(每次走一步,相当于之前两步抵消slow走的路程),那么走x步还会到达这个点,但是这两个指针这次都是每次走一步,所以一旦slow到达循环圈内,两个指针就开始汇合了。
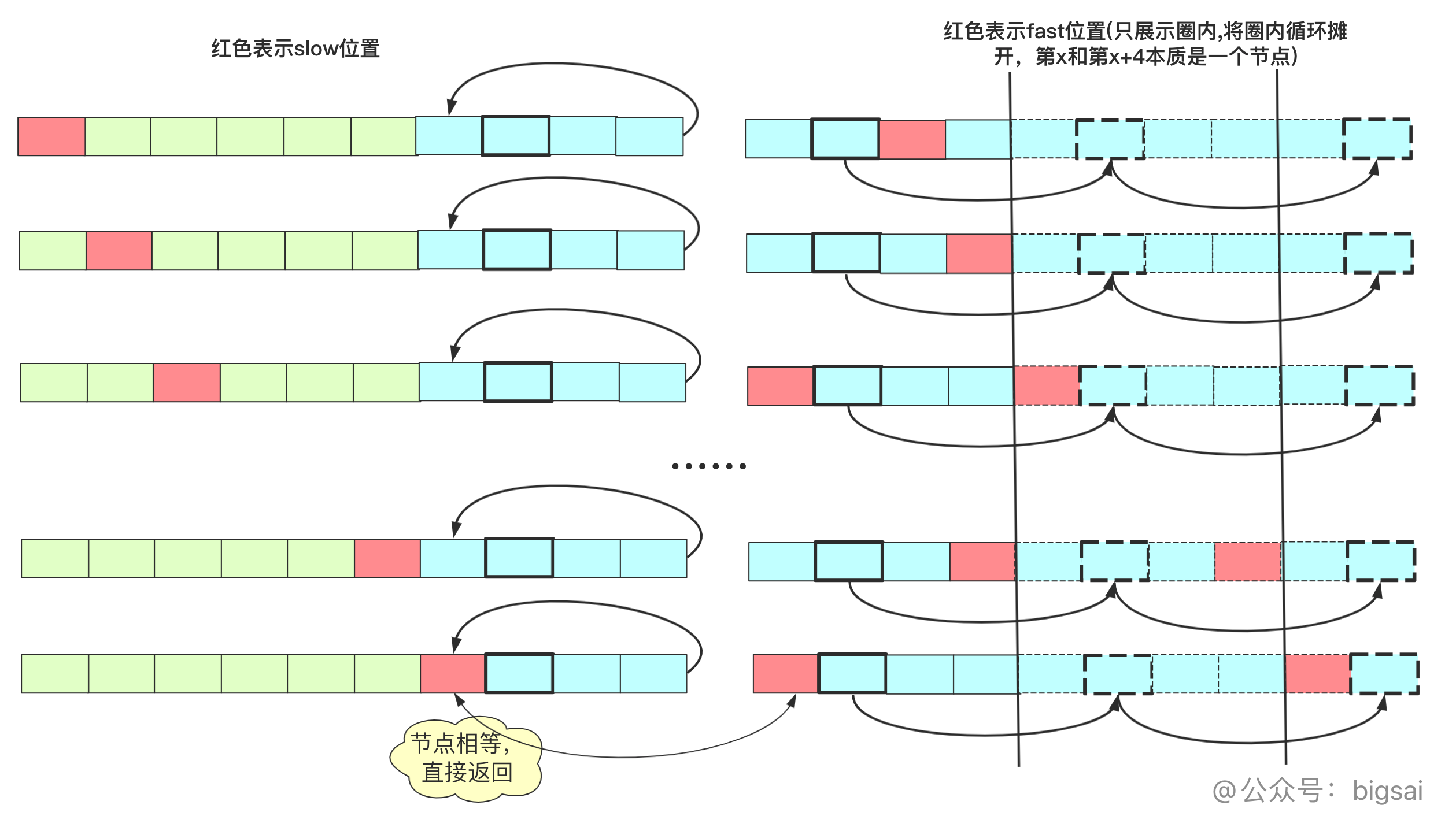
实现代码为:
public class Solution {
public ListNode detectCycle(ListNode head) {
boolean isloop=false;
ListNode fast=new ListNode(0);//头指针
ListNode slow=fast;
fast.next=head;
if(fast.next==null||fast.next.next==null)
return null;
while (fast!=null&&fast.next!=null) {
fast=fast.next.next;
slow=slow.next;
if(fast==slow)
{
isloop=true;
break;
}
}
if(!isloop)//如果没有环返回
return null;
ListNode team=new ListNode(-1);//头指针 下一个才是head
team.next=head;
while (team!=fast) {//slow 和fast 分别从起点和当前点出发
team=team.next;
fast=fast.next;
}
return team;
}
} 0X04两个栈实现队列
对应剑指offer09,题意为:
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
分析:
解决这个问题,要知道栈是什么,队列是什么,两种常见数据结构格式很简单,栈的特点就是:后进先出,队列的特点就是:先进先出,栈可以想象成一堆书本,越在上面的取的越早,上面来上面出(比喻一下);队列就是想象成排队买东西,只能后面进前面出,所以两者数据结构还是有区别的,虽然都是单个入口进出,但是栈进出口相同,而队列不同。
上面描述的是一个普通栈和队列的数据结构,这里面让我们用两个栈实现一个队列的操作,这里比较容易想的方案就是其中一个栈stack1用作数据存储,插入尾时候直接插入stack1,而删除头的时候将数据先加入到另一个栈stack2中,返回并删除栈顶元素,将stack2顺序加入stack1中实现一个复原,但是这样操作插入时间复杂度为O(1),删除时间复杂度为O(n)比较高。
实现方式也给大家看下:
class CQueue {
Stack<Integer>stack1=new Stack<>();
Stack<Integer>stack2=new Stack<>();
public CQueue() {
}
public void appendTail(int value) {
stack1.push(value);
}
public int deleteHead() {
if(stack1.isEmpty())
return -1;
while (!stack1.isEmpty())
{
stack2.push(stack1.pop());
}
int value= stack2.pop();
while (!stack2.isEmpty())
{
stack1.push(stack2.pop());
}
return value;
}
} 这样的时间复杂度是不被喜欢的,因为删除太鸡儿耗时了,每次都要折腾一番,有没有什么好的方法能够让删除也方便一点呢?
有啊,stack1可以顺序保证顺序插入,stack1数据放到stack2中可以保证顺序删除,所以用stack1作插入,stack2作删除,因为题目也没要求数据必须放到一个容器中,所以就这样组合使用,完美perfect!
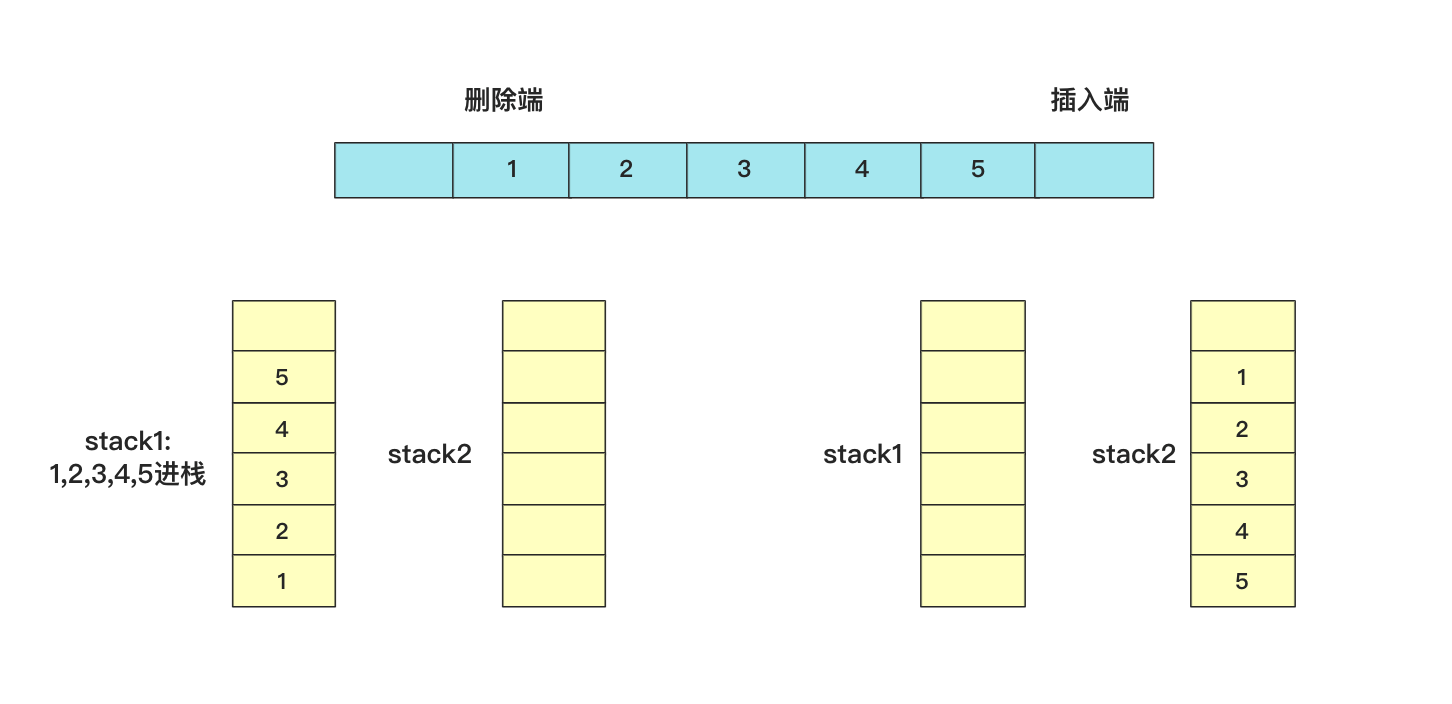
具体实现的时候,插入直接插入到stack1中,如果需要删除从stack2中栈顶删除,如果stack2栈为空那么将stack1中数据全部添加进来(这样又能保证stack2中所有数据是可以顺序删除的了),下面列举几个删除的例子
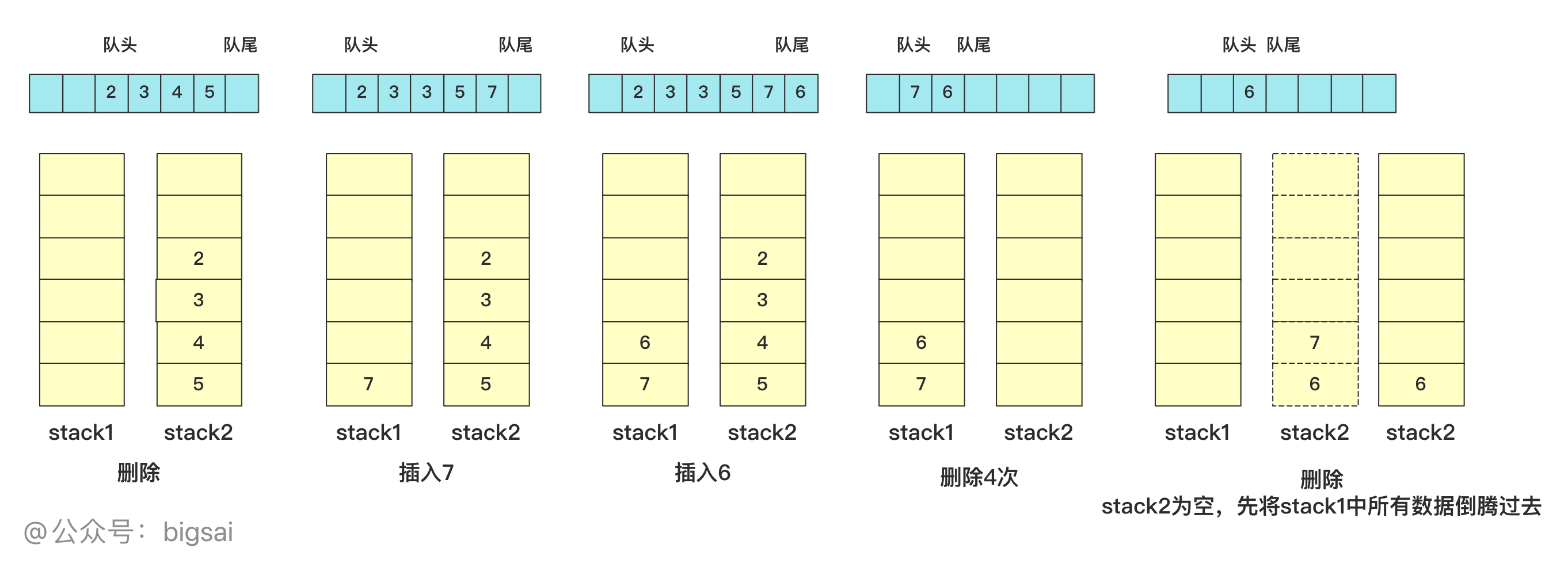
其实就是将数据分成两个部分,一部分用来插入,一部分用来删除,删除的那个栈stack2空了添加所有stack1中的数据继续操作。这个操作插入删除的时间复杂度是O(1),具体实现的代码为:
class CQueue {
Deque<Integer> stack1;
Deque<Integer> stack2;
public CQueue() {
stack1 = new LinkedList<Integer>();
stack2 = new LinkedList<Integer>();
}
public void appendTail(int value) {
stack1.push(value);
}
public int deleteHead() {
// 如果第二个栈为空 将stack1数据加入stack2
if (stack2.isEmpty()) {
while (!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
} //如果stack2依然为空 说明没有数据
if (stack2.isEmpty()) {
return -1;
} else {//否则删除
int deleteItem = stack2.pop();
return deleteItem;
}
}
} 0X05二叉树层序(锯齿)遍历
二叉树的遍历,对应力扣102,107,103.
详细分析:
如果普通二叉树层序遍历,也不是什么困难的问题,但是它会有个分层返回结果的操作,就需要你详细考虑了。
很多人会用两个容器(队列)进行分层的操作,这里其实可以直接使用一个队列,我们首先记录枚举前队列大小len,然后根据这个大小len去枚举遍历就可以得到完整的该层数据了。
还有一个难点就是二叉树的锯齿层序(也叫之字形打印),第一趟是从左往右,第二趟是从右往左,只需要记录一个奇偶层数进行对应的操作就可以了。

这里就拿力扣103二叉树的锯齿形层序遍历作为题板给大家分享一下代码:
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> value=new ArrayList<>();//存储到的最终结果
if(root==null)
return value;
int index=0;//判断
Queue<TreeNode>queue=new ArrayDeque<>();
queue.add(root);
while (!queue.isEmpty()){
List<Integer>va=new ArrayList<>();//临时 用于存储到value中
int len=queue.size();//当前层节点的数量
for(int i=0;i<len;i++){
TreeNode node=queue.poll();
if(index%2==0)//根据奇偶 选择添加策略
va.add(node.val);
else
va.add(0,node.val);
if(node.left!=null)
queue.add(node.left);
if(node.right!=null)
queue.add(node.right);
}
value.add(va);
index++;
}
return value;
} 0X06 二叉树中后序遍历(非递归)
二叉树的非递归遍历也是考察的重点,对于中序后序遍历递归实现很简单,非递归实现起来还是要点技巧的哦。
详细分析:
对于二叉树的中序遍历,其实就是正常情况第二次访问该节点的时候才抛出输出(第一次数前序),这样我们枚举每个节点第一次不能删除,需要先将它存到栈中,当左子节点处理完成的时候在抛出访问该节点。

核心也就两步,叶子节点左右都为null,也可满足下列条件:
- 枚举当前节点(不存储输出)并用栈存储,节点指向左节点,直到左孩子为null。
- 抛出栈顶访问。如果有右节点,访问其右节点重复步骤1,如有没右节点,继续重复步骤2抛出。
实现代码为:
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer>value=new ArrayList<Integer>();
Stack<TreeNode> q1 = new Stack();
while(!q1.isEmpty()||root!=null)
{
while (root!=null) {
q1.push(root);
root=root.left;
}
root=q1.pop();//抛出
value.add(root.val);
root=root.right;//准备访问其右节点
}
return value;
}
} 而后序遍历按照递归的思路其实一般是第三次访问该节点是从右子节点回来才抛出输出,这个实现起来确实有难度。但是具体的实现,我们使用一个pre节点记录上一次被抛出访问的点,如果当前被抛出的右孩子是pre或者当前节点右为null,那么就将这个点抛出,否则说明它的右侧还未被访问需要将它"回炉重造",后面再用!如果不理解可以看前面的详细介绍。
具体实现的代码为:
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
TreeNode temp=root;//枚举的临时节点
List<Integer>value=new ArrayList<>();
TreeNode pre=null;//前置节点
Stack<TreeNode>stack=new Stack<>();
while (!stack.isEmpty()||temp!=null){
while(temp!=null){
stack.push(temp);
temp=temp.left;
}
temp=stack.pop();
if(temp.right==pre||temp.right==null)//需要弹出
{
value.add(temp.val);
pre=temp;
temp=null;//需要重新从栈中抛出
}else{
stack.push(temp);
temp=temp.right;
}
}
return value;
}
} 当然,后序遍历也有用前序(根右左)的前序遍历结果最后翻转一下的,但面试官更想考察的还是上面提到的方法。
0X07 跳台阶(斐波那契、爬楼梯)
爬楼梯、跳台阶是一个经典问题,对应剑指offer10和力扣70题,题目的要求为:
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?注意:给定 n 是一个正整数。
分析:
这个问题入门级别dp,分析当前第k阶的结果,每个人可以爬1个或者2个台阶,那么说明它可能是由k-1或者k-2来的,所以就是两个子情况的叠加(需要特殊考虑一下初始情况),这个思路有人会想到递归,没错用递归确实可以解决但是用递归效率较低(因为这个是个发散的递归一个拆成两个),使用记忆化搜索会稍微好一些。
但是dp是比较好的方法,核心状态转移方程为:dp[i]=dp[i-1]+dp[i-2],有些空间优化的那就更好了,因为只用到前两个值,所以完全可以用三个值重复使用节省空间。
class Solution {
public int climbStairs(int n) {
if(n<3)return n;
int dp[]=new int[n+1];
dp[1]=1;
dp[2]=2;
for(int i=3;i<n+1;i++)
{
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
public int climbStairs(int n) {
int a = 0, b = 0, c = 1;
for (int i = 1; i <= n; i++) {
a = b;
b = c;
c = a + b;
}
return c;
}
} 当然,有的数据很大求余的跳台阶,可以用矩阵快速幂解决,但是这里就不介绍啦,有兴趣可以详细看看。
0X08 TOPK问题
TOPK问题真的非常经典,通常问的有最小的K个数,寻找第K大都是TOPK这种问题,这里就用力扣215寻找数组第K大元素作为板子。
详细分析:
TOPK的问题解决思路有很多,如果优化的冒泡或者简单选择排序,时间复杂度为O(nk),使用优化的堆排序为O(n+klogn),不过掌握快排的变形就可以应付大体上的所有问题了(面试官要是让你手写堆排序那真是有点难为你了)。
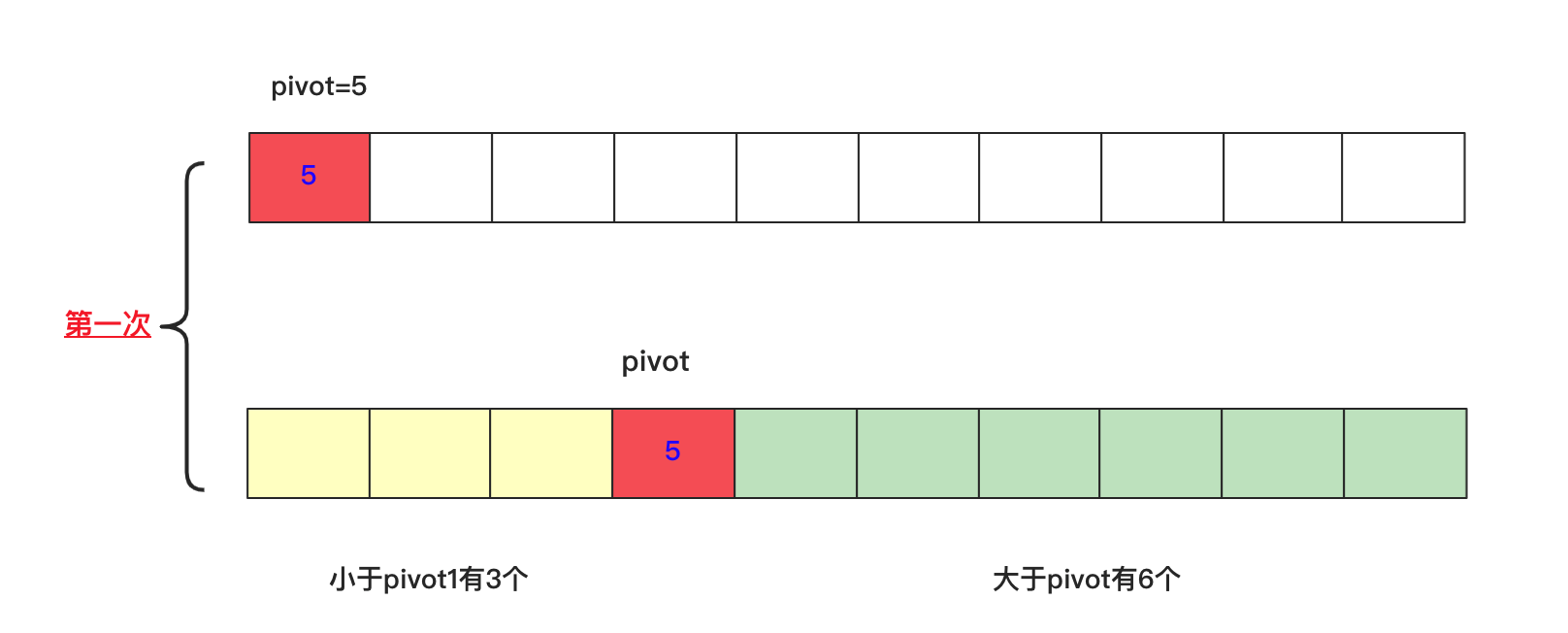
快排每次确定一个数pivot位置,将数分成两部分:左面的都比这个数pivot小,右面的都比这个数pivot大,这样就可以根据这个k去判断刚好在pivot位置,还是左侧还是右侧?可以压缩空间迭代去调用递归最终求出结果。
很多人为了更快过测试样例将这个pivot不选第一个随机选择(为了和刁钻的测试样例作斗争),不过这里我就选第一个作为pivot了,代码可以参考:
class Solution {
public int findKthLargest(int[] nums, int k) {
quickSort(nums,0,nums.length-1,k);
return nums[nums.length-k];
}
private void quickSort(int[] nums,int start,int end,int k) {
if(start>end)
return;
int left=start;
int right=end;
int number=nums[start];
while (left<right){
while (number<=nums[right]&&left<right){
right--;
}
nums[left]=nums[right];
while (number>=nums[left]&&left<right){
left++;
}
nums[right]=nums[left];
}
nums[left]=number;
int num=end-left+1;
if(num==k)//找到k就终止
return;
if(num>k){
quickSort(nums,left+1,end,k);
}else {
quickSort(nums,start,left-1,k-num);
}
}
} 0X09 无重复的最长子串(数组)
这个问题可能是个字符串也可能是数组,但是道理一致,无重复字符的最长子串和最长无重复子数组本质一致。
题目要求为:给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
分析:
此题就是给一个字符串让你找出最长没有重复的一个子串。 要搞清子串和子序列的区别:
子串:是连续的,可以看成原串的一部分截取。
子序列:不一定是连续的,但是要保证各个元素之间相对位置不变。
那么我们如何处理呢?
暴力查找,暴力查找当然是可以的,但是复杂度过高这里就不进行讲解了。这里选择的思路是滑动窗口,滑动窗口,就是用一个区间从左往右,右侧先进行试探,找到区间无重复最大值,当有重复时左侧再往右侧移动一直到没重复,然后重复进行到最后。在整个过程中找到最大子串即可。
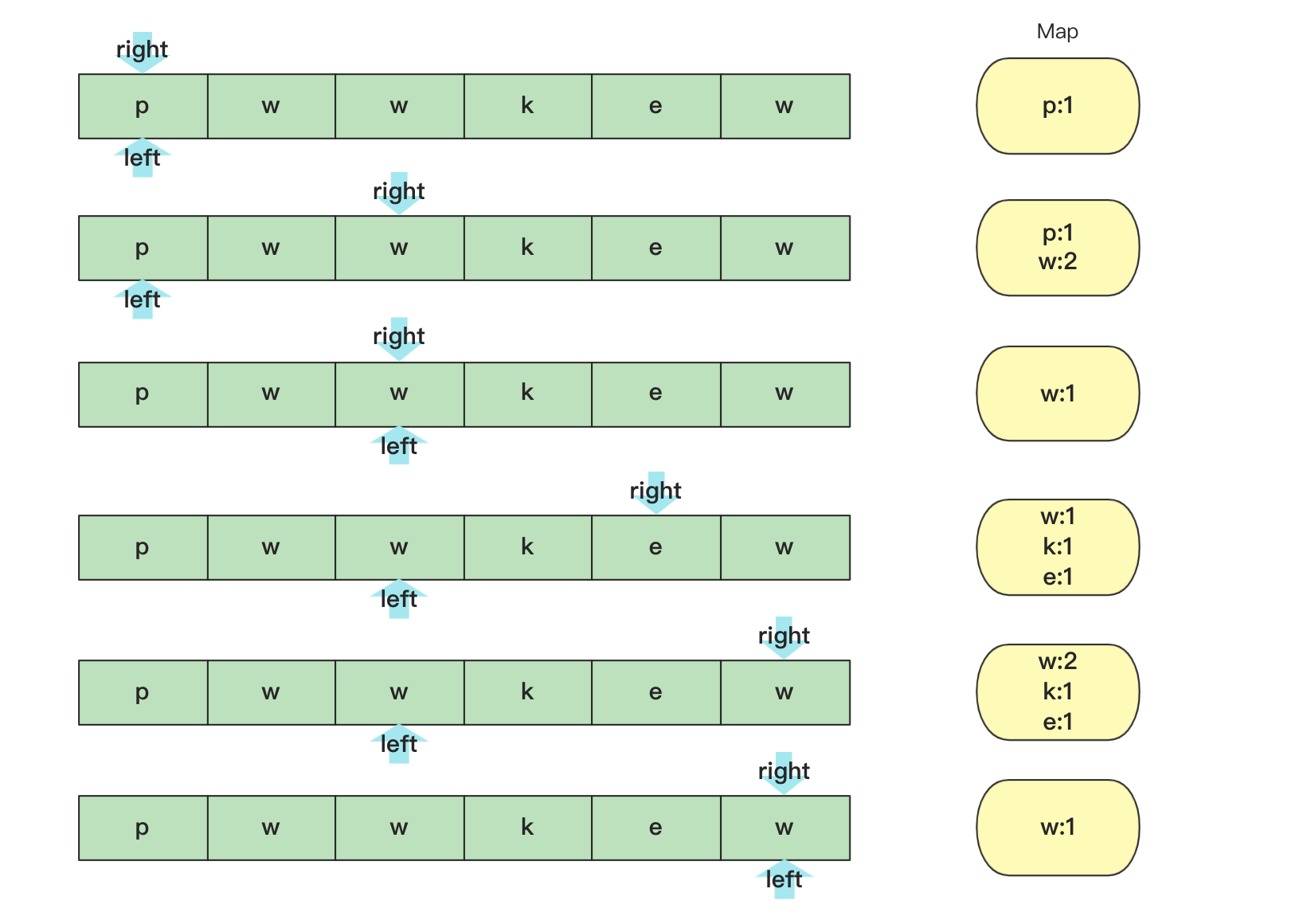
具体实现时候可以用数组替代哈希表会快很多:
class Solution {
public int lengthOfLongestSubstring(String s) {
int a[]=new int[128];
int max=0;//记录最大
int l=0;//left 用i 当成right,当有重复左就往右
for(int i=0;i<s.length();i++)
{
a[s.charAt(i)]++;
while (a[s.charAt(i)]>1) {
a[s.charAt(l++)]--;
}
if(i-l+1>max)
max=i-l+1;
}
return max;
}
} 0X10 排序
不会真的有人以为用个Arrays.sort()就完事了吧,手写排序还是很高频的,像冒泡、插入这些简单的大家相比都会,像堆排序、希尔、基数排序等考察也不多,比较高频的就是快排了,这里额外奖励一个也很高频的归并排序,两个都是典型分治算法,也可以将快排和前面的TOPK问题比较一番。
排序详细的十大排序都有详细讲过,大家可以自行参考
快排:
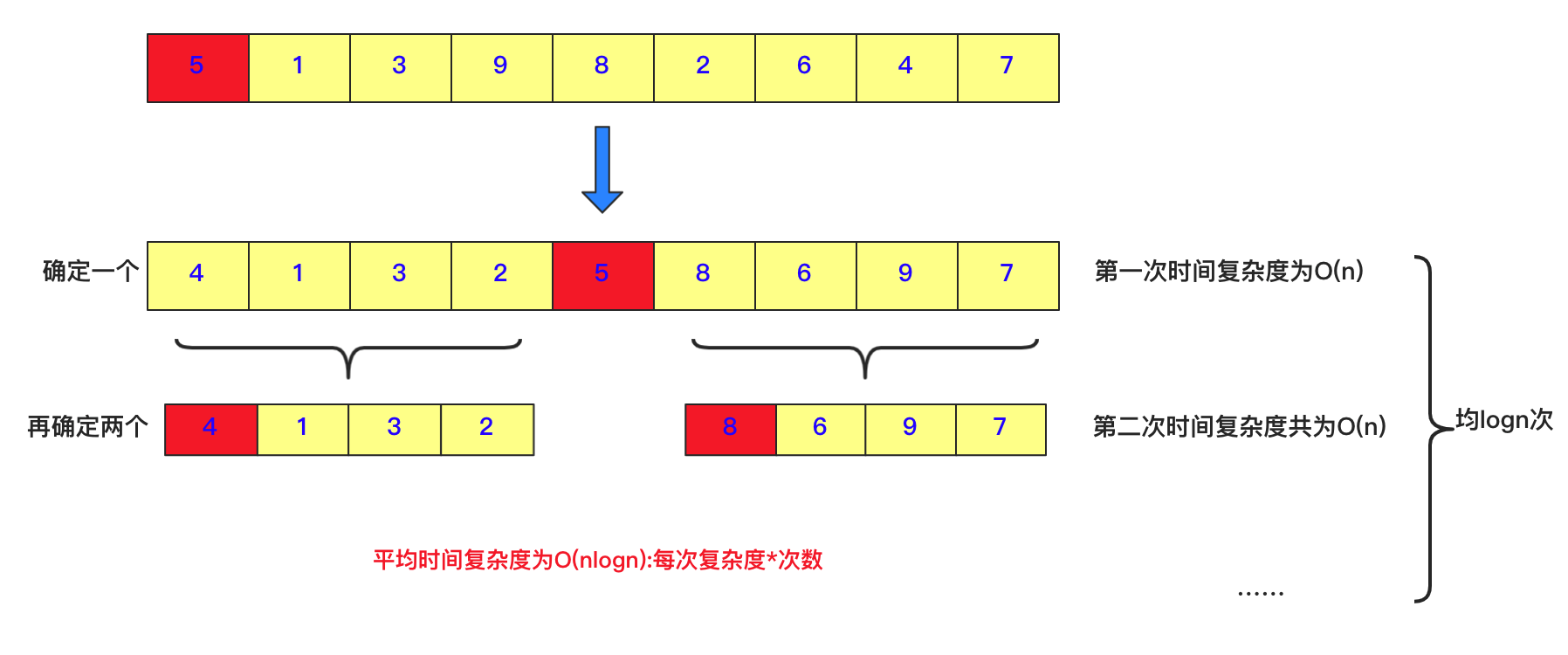
具体实现:
public void quicksort(int [] a,int left,int right)
{
int low=left;
int high=right;
//下面两句的顺序一定不能混,否则会产生数组越界!!!very important!!!
if(low>high)//作为判断是否截止条件
return;
int k=a[low];//额外空间k,取最左侧的一个作为衡量,最后要求左侧都比它小,右侧都比它大。
while(low<high)//这一轮要求把左侧小于a[low],右侧大于a[low]。
{
while(low<high&&a[high]>=k)//右侧找到第一个小于k的停止
{
high--;
}
//这样就找到第一个比它小的了
a[low]=a[high];//放到low位置
while(low<high&&a[low]<=k)//在low往右找到第一个大于k的,放到右侧a[high]位置
{
low++;
}
a[high]=a[low];
}
a[low]=k;//赋值然后左右递归分治求之
quicksort(a, left, low-1);
quicksort(a, low+1, right);
} 归并排序:
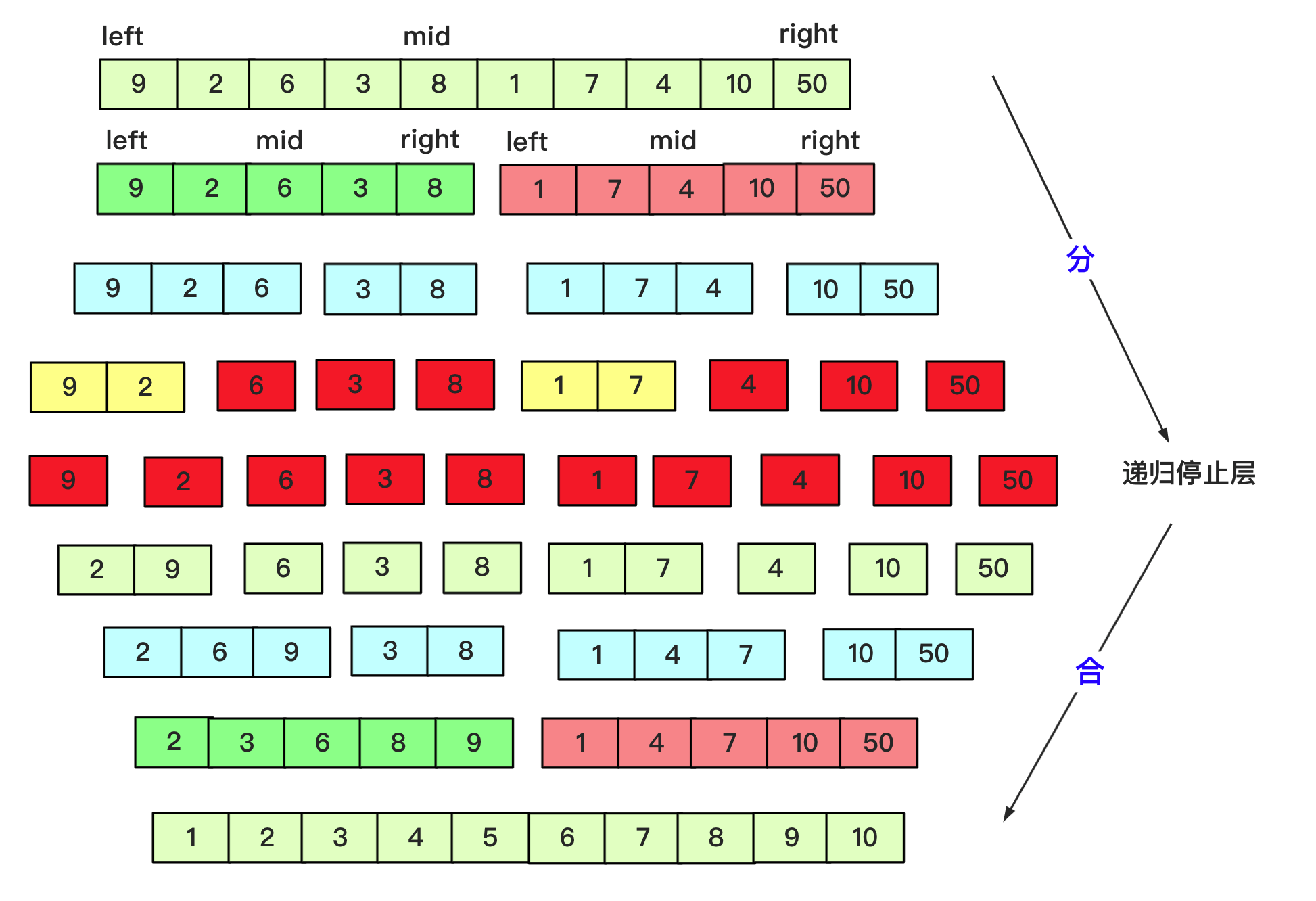
实现代码为:
private static void mergesort(int[] array, int left, int right) {
int mid=(left+right)/2;
if(left<right)
{
mergesort(array, left, mid);
mergesort(array, mid+1, right);
merge(array, left,mid, right);
}
}
private static void merge(int[] array, int l, int mid, int r) {
int lindex=l;int rindex=mid+1;
int team[]=new int[r-l+1];
int teamindex=0;
while (lindex<=mid&&rindex<=r) {//先左右比较合并
if(array[lindex]<=array[rindex])
{
team[teamindex++]=array[lindex++];
}
else {
team[teamindex++]=array[rindex++];
}
}
while(lindex<=mid)//当一个越界后剩余按序列添加即可
{
team[teamindex++]=array[lindex++];
}
while(rindex<=r)
{
team[teamindex++]=array[rindex++];
}
for(int i=0;i<teamindex;i++)
{
array[l+i]=team[i];
}
} 结语
好了,今天给大家分享的10个问题,是真的在面试中非常非常高频,我敢说平均每两次面试就得遇到这里面的其中一个题(毫不夸张)!
虽说题海很深学不完,但是学过缓存的都知道要把热点数据放缓存,考过试的都知道要把必考点掌握……这十个问题已经送到嘴边。
当然,这只是非常非常高频的问题,要想拿捏笔试,肯定还要不断积累、刷题。
原创不易,求个关注、点赞,谢谢!个人公众号:bigsai,坚持分享,我们下次再见!


 查看3道真题和解析
查看3道真题和解析

