题解 | #孤独的数组#

原文传送门

分析

根据算术基本定理，任何数一定都可以被分解成质数的乘积，因此对于每个结点的值，我们可以先预处理出每个结点的最小质因子，每次讨论是否执行除去这个最小质因子$pp$的操作： ① 如果要除$pp$，就必须将这个质因子除干净，同时记录除这个$pp$进行了多少次操作 ② 如果不除$pp$，那么子节点就必须要执行除$pp$的操作，否则就有公共质因子$pp$，但是即使当前子节点没有执行除$pp$的操作，我们还是要将当前子节点的质因子$pp$除去，因为只有这样才能在除去所有$pp$后继续讨论剩余值的最小质因子，我们不除$pp$只是不记录操作次数。比如对于$9898$，我们在讨论最小质因子$77$的时候，如果不执行除$77$操作，那么我们还是要将$77$显式的全部除去变成$44$，然后继续讨论$44$的最小质因子$22$

操作过程理解

假设我们当前在考虑结点$uu$，它的权值为$ww$，那么$ww$的所有质因子不一定就是子节点的所有质因子，即对第$uu$个数操作完只能保证整个树中任意一条边连接的两个点权值的公共质因子没有$uu$的质因子，但是其他点还可能有其他质因子，所以每个结点都要作为起点去将它的所有质因子操作一遍 其实也就是说我们是枚举每个结点，然后分解出每个结点权值的质因数$pp$来求让整个树满足不存在边上两点有这个质因数$pp$的最小操作次数 因为同一个数对于质因子$pp$只计数一次除了$pp$多少次，因此用$pp$处理第$ii$个数的时候我们要确保第$ii$个数还没有被这个质因数给操作过，可以开一个$st[i][p]st[i][p]$(二维$1e51e5$爆内存)，因为每个$w[i]w[i]$的质因数都是离散的，因此可以考虑用二维$setset$<$intint$>来标记

树形$dpdp$

状态表示：f[i][2]
  集合：f[i][0]表示结点i不除p这个质因子，且让i和它的所有连接点没有公共质因子p的最小操作次数
        f[i][1]表示结点i除p这个质因子，让i和它的连接点没有公共质因子p的最小操作次数
  属性：Min
状态计算：

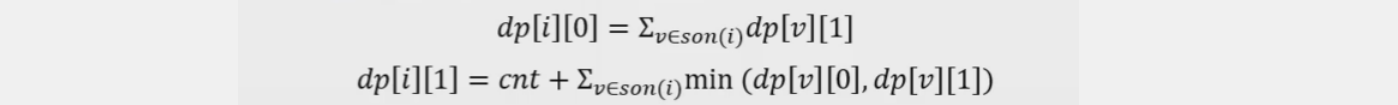
即对当前结点值讨论它的质因子p的时候，如果当前结点不除p(f[cur][0])，那么它的所有连接点就要都除p(f[son][1])
而如果当前结点除p(f[cur][1])，那么就要记录它一共除了多少个p(执行了多少次操作)，而它的所有子节点除p还是不除p
均可，要取其最小值(min(f[son][1], f[son][0])

答案

对于每个点$uu$的某个质因子$pp$，我们其实都是去讨论让整个树的任意一条边连接的两个点没有公共质因子$pp$的最少操作数，因此每次都要加上$min(f[i][0],f[i][1])min(f[i][0],f[i][1])$

$CodeCode$

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10, M = N * 2;
int f[N][2];
int h[N], e[M], w[M], ne[M], idx;
bool st[N];
int minp[N];
set<int> book[N];
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u, int p)  // 讨论结点u对质数p的操作
{
    book[u].insert(p);  // 标记结点u已经讨论过对质数u的操作
    int curw = w[u], cnt = 0;
    while (curw % p == 0) curw /= p, cnt ++;  // 记录当前点最多可以做多少次除p操作
    int sum0 = 0, sum1 = 0;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!book[j].count(p) && w[j] % p == 0)
        {
            dfs(j, p);
            sum0 += f[j][1];  // 当前结点不操作p，那么子节点肯定要操作
            sum1 += min(f[j][0], f[j][1]);  // 当前结点操作p，那么子节点均可
        }
    }
    f[u][0] = sum0;
    f[u][1] = sum1 + cnt;
}
int main()
{
    int n; cin >> n;
    for (int i = 2; i <= N; i ++)
        if (!st[i])  // 如果这个数没有别筛掉，就拿它去筛其他的质数
            for (int j = i; j <= N; j += i) st[j] = true, minp[j] = i;  // j一定会最先被它最小的质因数i给筛掉
    for (int i = 1; i <= n; i ++) cin >> w[i];
    memset(h, -1, sizeof h);
    for (int i = 0, a, b; i < n - 1; i ++) cin >> a >> b, add(a, b), add(b, a);
    int ans = 0;
    for (int i = 1; i <= n; i ++)  // 以每个点为起点去操作其他点
    {
        while (w[i] != 1)  // 如果这个点的所有质因数还没有考虑完
        {
            int p = minp[w[i]];  // p为w[i]的最小质因子
            if (!book[i].count(p))  // 如果点i还没有操作过质因子p才考虑
            {
                dfs(i, p);
                ans += min(f[i][0], f[i][1]);  // 累加上让整个树不具有公共质因子p的最小操作次数 
            }
            while (w[i] % p == 0) w[i] /= p;   // 将p全部除去
        }
    }
    printf("%d", ans);
    return 0;
}