题解 | #在二叉树中找到两个节点的最近公共祖先#
在二叉树中找到两个节点的最近公共祖先
http://www.nowcoder.com/practice/e0cc33a83afe4530bcec46eba3325116
题目描述
给定我们一颗二叉树,然后给我们两个点,让我们去找这两个点的最近公共祖先,就是他们一起向上查找,第一个相遇的点
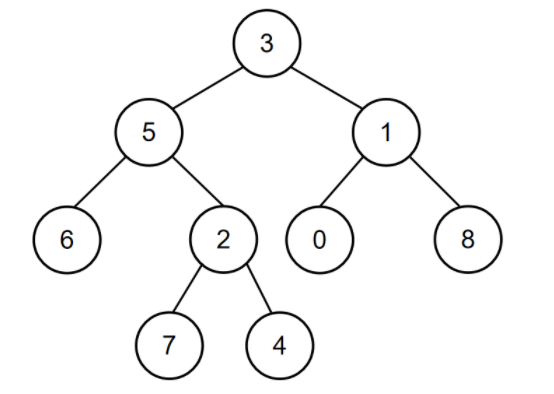
这样的一棵树,比如我们5和1的最近公共祖先就是3
其实这个问题是一个非常经典的问题,难度不是很高
题解
解法一:递归法
实现思路
这里引入一下: 我这里的p节点就是我们o1节点, q节点就是我们的o2节点, 后面就直接用p和q代替了
我们可以先理解一下祖先的概念:
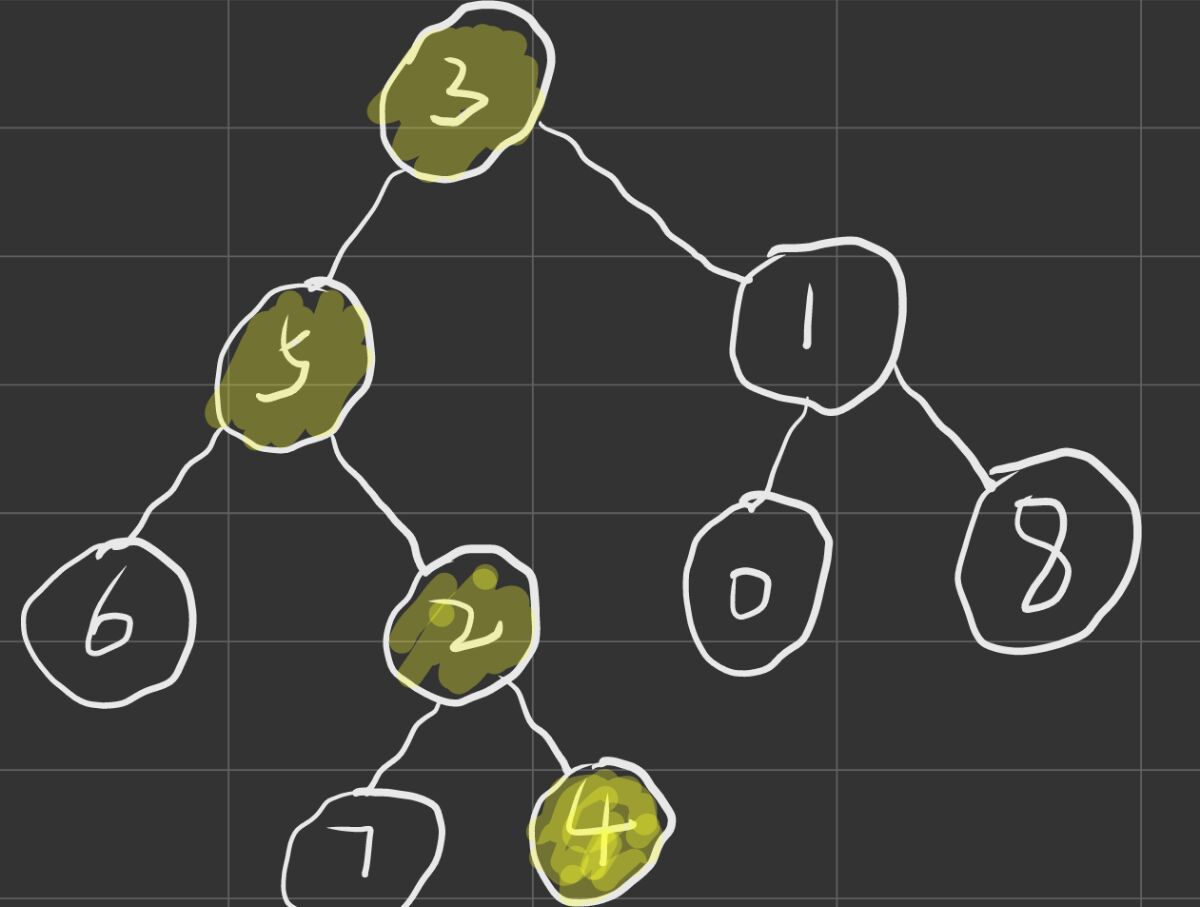
涂黄色的点就是我们的节点4的所有祖先
然后我们可以考虑一下,如果假设我们的x节点是我们p和q的最近公共祖先,那么分为三种情况
- p和q都在root的子树中,并且分列root的异侧
- p == root,q在root的子树中
- q == root,p在root的子树中
然后我们可以直接递归,如果遇到节点p或者q的时候返回
然后我们看一下我们的递归条件:
- 如果我们到达叶子节点,返回返回nullptr
- 如果root等于p或q,返回root
我们每次递归左右节点分别返回left和right
然后我们根据返回值来分类讨论
- 如果左右同时为空:root的左右子树都没有p和q,返回空
- 如果同时不空,就是在root的异侧,root就是最近公共祖先
- 如果一个为空一个不为空:那么他们都不在为空的那颗子树里面,然后我们可以得到要么是一个在返回值不空的子树中,要么就是都在不空中
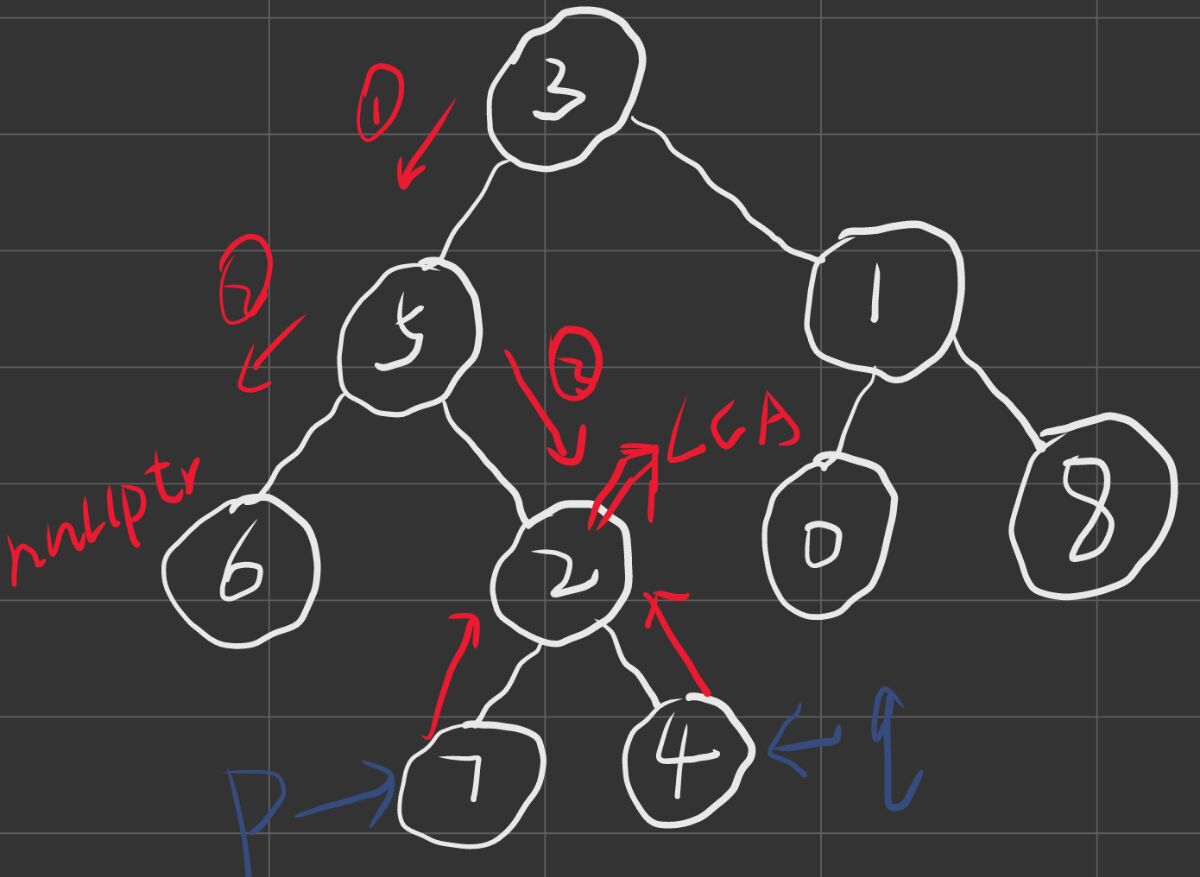
图中蓝色画出来的就是我们要找的p和q节点,然后我们红色的是遍历的路线,最后得到2就是最近公共祖先
代码实现
class Solution {
public:
int lowestCommonAncestor(TreeNode *root, int o1, int o2) {
if (root == nullptr) return 0;
// 如果是空的就返回
if (root->val == o1 || root->val == o2) return root->val;
// 如果找到了节点,返回
int l = lowestCommonAncestor(root->left, o1, o2);
int r = lowestCommonAncestor(root->right, o1, o2);
// 左右子树遍历
if (l == 0) return r;
if (r == 0) return l;
// 右子树没找到就是在左子树,左子树没找到就是在右子树
return root->val;
}
};
时空复杂度分析
时间复杂度:
理由如下: 我们最差的情况下会遍历我们的所有的节点
空间复杂度:
理由如下: 我们最坏情况下, 二叉树会退化成为一条链, 我们的系统的递归栈的深度就是n
解法二: 存储父亲节点
实现思路
我们可以先找到这两个节点对应的树上的节点在哪里, 然后我们可以用哈希表存储所有节点的父亲, 然后我们就可以利用节点的父亲信息从p节点开始不断向上跳,并记录已经访问过的节点,再从q节点往上跳,如果碰到已经访问过的节点,那么这个节点就是我们的答案
- 根节点开始遍历整颗二叉树, 用哈希表记录每一个节点的父亲节点的指针
- 从p节点开始不断向着祖先移动,并用数据结构记录已经访问过的节点
- 然后从另一个点也开始移动,如果有已经被访问的点,那么就是公共祖先
代码实现
class Solution {
unordered_map<int, TreeNode *> fa;
unordered_map<int, bool> vis;
TreeNode *p, *q;
public:
void init(TreeNode *root, int o1, int o2) {
if (root == nullptr) return;
if (root->val == o1) p = root;
if (root->val == o2) q = root;
init(root->left, o1, o2);
init(root->right, o1, o2);
}
// 找到我们对应的树上的节点应该是哪一个
void dfs(TreeNode *root) {
if (root->left != nullptr) {
fa[root->left->val] = root;
dfs(root->left);
}
if (root->right != nullptr) {
fa[root->right->val] = root;
dfs(root->right);
}
}
// 遍历我们整颗树, 把我们需要的信息存储下来
int lowestCommonAncestor(TreeNode *root, int o1, int o2) {
init(root, o1, o2);
fa[root->val] = nullptr;
dfs(root);
while (p != nullptr) {
vis[p->val] = true;
p = fa[p->val];
}
// 跑一次我们p的路径
while (q != nullptr) {
if (vis[q->val]) return q->val;
q = fa[q->val];
}
// 跑一次我们q的路径, 如果有一样的就输出
return 0;
}
};
时空复杂度分析
时间复杂度:
理由如下: 我们所有节点都会被访问一次, 然后我们p和q向上跳的时候,经过的节点不会超过n个,所以我们的时间复杂度就是
空间复杂度:
理由如下: 我们最坏情况下, 二叉树会退化成为一条链, 我们的系统的递归栈的深度就是n, 然后我们的哈希表存储也需要空间, 所以最后就是
主要是机试题目的题目讲解和做法



