排序-快排、冒泡、插入、选择、归并排序
快排、冒泡、插入、归并排序实现
1. 基础排序
1.1. 快速排序
基本思想:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据小。然后再按此方法对两部分数据分别进行快速排序,整个排序过程 递归 进行,以此达到整个数据变成有序序列。
基于这个思想,可以写出下面的代码:
class Solution:
def sortArray(self, nums: List[int]):
if not nums or len(nums) == 0:
return []
if len(nums) == 1: # 递归终止条件
return nums
ref = nums[0] # 基准值
left_part = [] # 保存比基准值小的元素
right_part = [] # 保存比基准值大的元素
for i in range(1, len(nums)):
if nums[i] < ref:
left_part.append(nums[i])
else:
right_part.append(nums[i])
# 对左右两部分分别递归执行该操作
return self.sortArray(left_part)+[ref]+self.sortArray(right_part) 存在问题:通过上述代码发现一个问题,每次递归都重新申请left_part和right_part,这在很大程度上浪费了空间。
优化思路:由于left_part和right_part中存储的内容是nums中的内容,只不过是对nums中的数值进行了分类。因此可以考虑在nums中更新数组位置,从而达到小于基准值的元素存放在nums的前半部分,大于基准值的元素存放在后半部分。如下图:
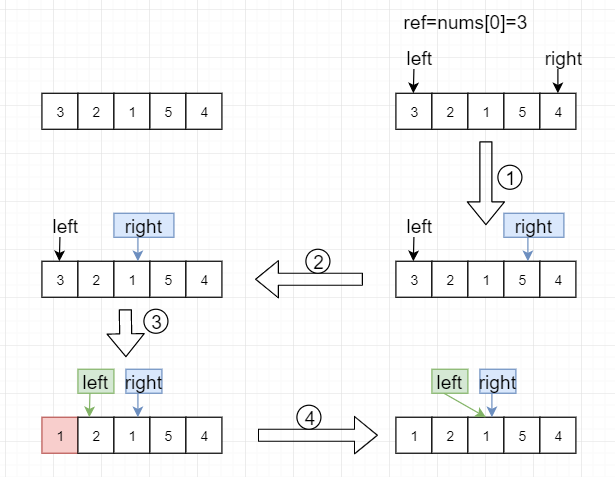
步骤:
保存数组第一个元素在ref中,同时定义left和right指针。
- nums[right]=4>ref,表示当前元素大于基准值,此时直接向前移动right,不用改变元素位置。
- nums[right]=5>ref,此时直接向前移动right,不用改变元素位置
- nums[right]=1<ref, 此时right指向的元素小于基准值,此时应该放在nums数组的前面部分,因此与将right指针指向的元素存放在left指向的位置(由于left指向的元素是已经保存在了ref中,所以不用担心被覆盖),同时left向后移动。
- nums[left]=2<ref, 此时表示当前元素小于ref,就应该放在nums的前面位置,因此不用更新元素位置,直接left指向下一个位置即可。
说明:
- 首先,比较right指向的位置与ref的大小,如果nums[right]>ref,此时就right前移,然后继续比较即可。
- 如果nums[right]<ref,就将right之前的元素与left指向的元素交换位置,然后开始比较left指向位置的元素与ref的大小。
- 函数中定义的flag是为了控制移动的指针,当flag=True的时候,比较right指向的元素。当flag=left的时候,比较left指向的元素。
class Solution:
def sortArray(self, nums):
if not nums or len(nums) == 0:
return []
if len(nums) == 1: # 递归终止条件
return nums
ref = nums[0] # 基准值
left = 0
right = len(nums)-1
flag = True
while left < right:
if flag:
if nums[right] < ref:
nums[left] = nums[right]
left += 1
flag = False
else:
right -= 1
else:
if nums[left] > ref:
nums[right] = nums[left]
right -= 1
flag = True
else:
left += 1
return self.sortArray(nums[:left])+[ref]+self.sortArray(nums[left+1:]) 1.2. 冒泡排序
基本思想:重复走访要排序的数组,依次比较两个相邻的元素,如果顺序错误就交换,知道没有相邻元素需要交换,也就是说序列已经排序完成。
class Solution:
def sortArray(self, nums):
count = 0 # 记录遍历次数
while True:
flag = False # 每次遍历是否交换元素
for i in range(len(nums)-1-count):
# 每遍历一次都可以确定nums最后一个元素是最大值,因此就不用比较最后一个元素,所以可以减去count
j = i + 1
if nums[i] > nums[j]:
nums[j], nums[i] = nums[i], nums[j]
flag = True
count += 1
if not flag:
break
return nums 1.3. 插入排序
基本思想:对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
思路如下图: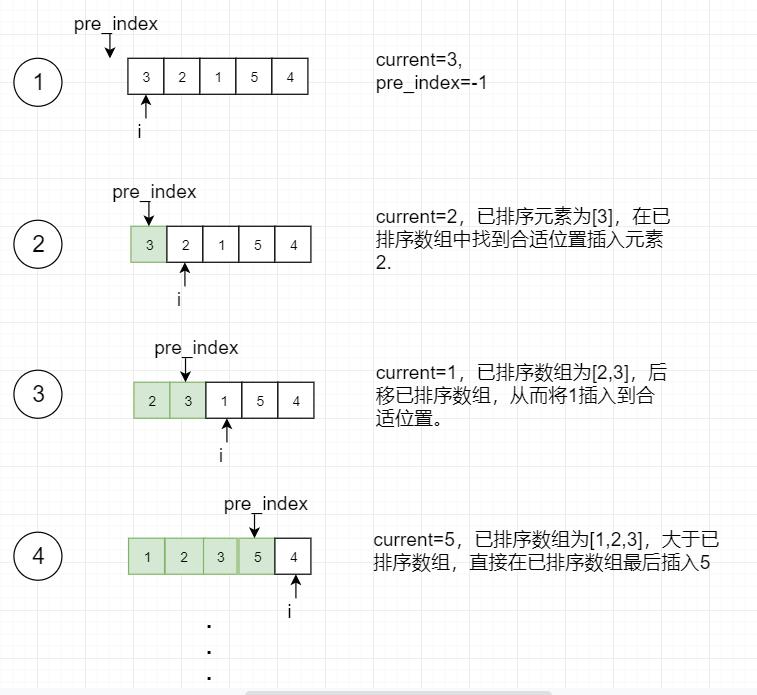
说明:
- current表示当前要排序的元素
- pre_index表示已排序元素的末尾元素的索引,从而能够遍历已排序数组,从而找到合适的插入位置。
class Solution:
def sortArray(self, nums):
for i in range(len(nums)):
current = nums[i] # 当前元素
pre_index = i - 1
while pre_index >= 0 and current < nums[pre_index]: # 移动数组元素,从而在合适的位置插入current
nums[pre_index+1] = nums[pre_index]
pre_index -= 1
nums[pre_index+1] = current
return nums 1.4. 选择排序
基本思想:第一次从待排序的数据元素中选出最小的元素,存放在序列的起始位置,然后再从剩余未排序的元素中寻找最小元素,放到已排序的序列的末尾,以此类推,知道全部待排序的数据元素的个数为零。
图形化过程如下图:
- right指向起始位置,right右侧表示未排序序列(包含right指向元素)
- 从right右侧选择最小元素1,然后存放在起始位置。right右移动一位。
- 从right右侧选择最小元素2,然后存放到已排序序列的后面。right右移一位。
- 重复过程,直到right移动到数组末尾即可。
class Solution:
def sortArray(self, nums):
# right指向未排序数组的起始元素
right = 0
for _ in range(len(nums)):
min_num = float('inf') # 保存最小值
min_num_i = -1 # 保存最小值索引
for i in range(right, len(nums)):
if nums[i] < min_num:
min_num = nums[i]
min_num_i = i
nums[right], nums[min_num_i] = nums[min_num_i], nums[right]
right += 1
return nums 1.5. 归并排序
基本思想:归并排序是建立在归并操作上的一种有效的排序算法,该算法采用经典的分治策略。
思路:先分再合。如下代码所示:
- 通过递归方式在sortArray中不断的切分数组。
- 在merge中合并数组
class Solution:
def sortArray(self, arr):
if len(arr) <= 1: # 递归终止条件,数组长度小于1
return arr
# 数组切分
import math
mid = math.floor(len(arr)/2)
left = arr[:mid]
right = arr[mid:]
# 合并
return self.merge(self.sortArray(left), self.sortArray(right))
def merge(self, left, right):
"""
合并操作,类似于2个有序链表合并为1个有序链表的思路
"""
result = [] # 保存合并之后的有序数组
while left and right:
if left[0] < right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
if left: # 如果执行到这里,表示right里面的数据已经全部添加到result里面去了,
# 这里直接把left中剩余元素添加到result中即可
result.extend(left)
if right:
result.extend(right)
return result  联想公司氛围 153人发布
联想公司氛围 153人发布