货郎(旅行售货员)问题:
某售货员要到若干城市去推销商品,已知各城市之间的路程(或旅费)。他要选定一条从驻地出发,经过每个城市一次,最后回到驻地的路线,使总的路程(或旅费)最小。
测试例子:
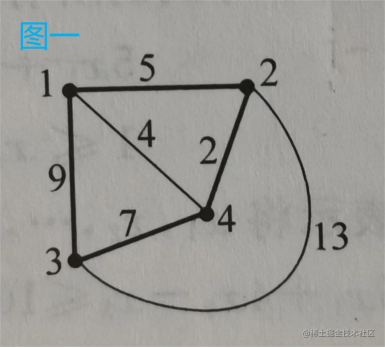
图一:1 2 5 1 3 9 1 4 4 2 3 13 2 4 2 3 4 7——从顶点1出发,共2个解
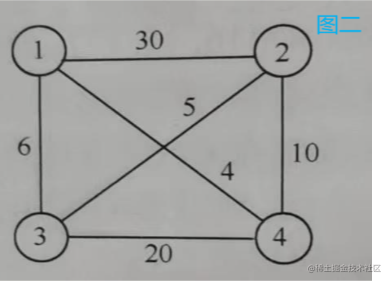
图二:1 2 30 1 3 6 1 4 4 2 3 5 2 4 10 3 4 20——从顶点1出发,共2个解
解法一:分支限界法
测试截图:


代码:
int main()
{
cout << "**********无向图,即任意两个顶点A、B,A—B和B—A距离相同\n";
cout << "默认顶点到自身距离为0,若两顶点不存在直接路径则对应权值为-1\n\n";
cout << "**********默认顶点从1~总顶点个数**********\n\n";
cout << "———————————————顶点个数为:";
cin >> N;
cout << "\n";
int** Map = InitMap(N);//初始化无向图
CreateMap(Map);//存入无向图信息
int** v = new int* [N - 1];//从顶点1出发,最多有N-1条最优路径
for (int i = 0; i < N - 1; i++)
{
v[i] = new int[N + 1];//由数组v带回最优路径
}
for (int i = 1; i < N; i++)//获取队列最大容量((N - 1)!*(N - 1) + 1)
{
MAXQ *= i;
}
MAXQ = MAXQ * (N - 1) + 1;
Mind = TSP(v, Map);//Mind为求得最短距离
if (Mind == -1)
{
cout << "不存在回路,即所给信息无法联通所有顶点!\n";
}
else
{
cout << "求得" << num << "条最优路径(从顶点1出发),如下:\n";
for (int i = 0; i < num; i++)
{
for (int j = 0; j < N; j++)
{
cout << v[i][j] << "—>";
}
cout << v[i][N];
cout << "———该路线距离为:" << Mind << endl;
}
}
system("pause");
return 0;
}
int TSP(int** v, int** map)//分支限界法求解
{
Queue queue;
InitQueue(queue);//初始化队列
int* MinOut = new int[N + 1];
int MinSum = 0;
for (int i = 1; i <= N; i++)//初始化
{
int min = -1;
for (int j = 1; j <= N; j++)//当j==i,表示顶点到自身,距离为0j!=i &&
{
if (map[i][j] != -1 && map[i][j] != 0 && (map[i][j] < min || min == -1))
min = map[i][j];
}
if (min == -1)//某顶点不存在出边,即地图不存在回路,无解
return -1;
MinOut[i] = min;//从顶点i出发的边的权值
MinSum += min;//各顶点最小出边权值之和
}
//初始化根结点
MinHeapNode E;
E.x = new int[N];
for (int i = 0; i < N; i++)
E.x[i] = i + 1;//初始顶点序列为1234
E.k = 0;
E.cc = 0;
E.rcost = MinSum;
int bestc = -1;
int judge = 1;
while (E.k < N - 1)//搜索深度到达最后一层
{
if (E.k == N - 2)//搜索深度到达倒数第二层
{
int s1, s2, ts;
s1 = map[E.x[N - 2]][E.x[N - 1]];//Vn-1——Vn的距离
s2 = map[E.x[N - 1]][E.x[0]];//Vn——V1的距离
ts = E.cc + s1 + s2;//E.cc:V1——Vn-1的距离
if (s1 != -1 && s2 != -1)
{
if (bestc == -1 || ts < bestc)//还未得到过解或找到更小值
{
bestc = ts;//当前最小值
E.cc = bestc;
E.k++;//进入下一层,即到达叶子结点
judge = PushQueue(queue, E);//结点E入队
if (judge == 0)//队已满
return bestc;
num = 1;
}
else
if (ts == bestc)//再次找到与当前最小值相等的路径
{
bestc = ts;//当前最小值
E.cc = bestc;
E.k++;//进入下一层,即到达叶子结点
judge = PushQueue(queue, E);//结点E入队
if (judge == 0)//队已满
return bestc;
num++;//
}
else
{
;//ts > bestc
}
}
else
delete[] E.x;//销毁E.x[]
}
else
{
for (int i = E.k + 1; i < N; i++)//从当前扩展(父)结点E.k(第E.k+1个顶点)出发,搜索子结点
{
int si = map[E.x[E.k]][E.x[i]];//V(E.k+1)——V(i+1)
if (si != -1)//当前结点E.k到子结点i+1存在直接路径
{
int cc = E.cc + si;
int rcost = E.rcost - MinOut[E.x[E.k]];//顶点E.x[E.k]加入路径,更新剩余顶点最小出边和
int b = cc + rcost;//计算当前路线距离
if (b < bestc || bestc == -1)//当前路线距离小于当前最优解,或暂未获得一个解
{
MinHeapNode M;//M用来记录此路线相关数据并将其入队
M.x = new int[N];
for (int j = 0; j < N; j++)//初始化路线,复制父结点路径(父节点包含根结点到父结点的最优路径)
M.x[j] = E.x[j];
M.x[E.k + 1] = E.x[i];//第E.k+1个顶点及前缀结点已确定,目前要确定第E.k+2个顶点(数组x[0:N-1]对应顶点V1:Vn,故x[E.k + 1]对应顶点V(E.k+2))
M.x[i] = E.x[E.k + 1];//通过循环,换遍所有子结点,父结点为当前路径中第E.k+1个顶点
M.k = E.k + 1;//进入下一层
M.cc = cc;//当前路径累加距离
M.rcost = rcost;
judge = PushQueue(queue, M);
if (judge == 0)//队已满
return bestc;
}
}
}
delete[] E.x;
}
judge = PopQueue(queue, E);
if (judge == 0)//队已空
{
cout << "\n未得到最优路径前队列已经为空,可能出错了!\n";//应该不会出现这种情况,但为避免发生意外,加上此判断
return bestc;
}
}
delete[] E.x;
judge = PopQueue(queue, E);//将第N-1层最后一个结点出队,剩余队员即为解
if (judge == 0)//队已空
{
cout << "\n未得到全部最优路径前队列已经为空,可能出错了!\n";//应该不会出现这种情况,但为避免发生意外,加上此判断
return bestc;
}
if (bestc != -1)//有回路
{
for (int i = 0; i < num; i++)//将最优解复制到v[i][0:N-1]
{
for (int j = 0; j < N; j++)
{
v[i][j] = E.x[j];
}
v[i][N] = v[i][0];//终点——起点,构成回路
delete[] E.x;
judge = PopQueue(queue, E);
if (judge == 0 && i < num - 1)//队已空
{
cout << "\n未得到全部最优路径前队列已经为空,可能出错了!\n";//应该不会出现这种情况,但为避免发生意外,加上此判断
break;
}
}
}
delete[] queue.Q;//销毁队列
return bestc;
}
#include<iostream>
using namespace std;
int N;//顶点个数
int Mind = -1;//最短距离
int MAXQ = 1;//队列最大容量((N-1)!*(N-1)+1),该公式是归纳得出的,应该没错,但以防万一,队列仍有对队满的判断
int num;//解的个数
//队列成员定义
struct MinHeapNode {
int cc;//当前路径累加距离
int rcost;//x[k:N-1]中顶点最小出边和
int k;//根节点到当前结点的路径为x[0:k]
int* x;//需要进一步搜索的结点是x[k+1:N+1]
};
//队列定义
struct Queue {
MinHeapNode* Q;
int front, rear;//队首指针和队尾指针
};
int** InitMap(int N);//初始化无向图
void CreateMap(int** map);//存入无向图信息
int TSP(int** v, int** map);//分支限界法求解
void InitQueue(Queue& q);//初始化队列
int EmptyQueue(Queue q);//判断队列是否为空
int PushQueue(Queue& q, MinHeapNode e);//结点e进队
int PopQueue(Queue& q, MinHeapNode& e);//结点e出队
int** InitMap(int N)//初始化地图
{
int** map = new int* [N + 1];
for (int i = 1; i <= N; i++)//0行0列不用,便于操作及理解代码
{
map[i] = new int[N + 1];
for (int j = 1; j <= N; j++)
{
if (i == j)
map[i][j] = 0;
else
map[i][j] = -1;
}
}
return map;
}
void CreateMap(int** map)//存入无向图信息
{
int anum;//待存入边数
int sV, eV, seW;//边起始点,边终点,边权值
cout << "边数(最多为:" << N * N << "条),请输入无向图中的边数:";
cin >> anum;
cout << "请输入详细数据,每条边的两个顶点及对应权值(>=0):\n";
for (int k = 1; k <= anum; k++)
{
cin >> sV >> eV >> seW;
map[sV][eV] = seW;
map[eV][sV] = seW;
}
cout << "恭喜您!地图已绘成!\n\n";
}
void InitQueue(Queue& q) //初始化队列
{
q.Q = new MinHeapNode[MAXQ];
q.front = 0;
q.rear = 0;
}
int EmptyQueue(Queue q)//队列判空
{
return q.front == q.rear;//头结点与尾结点在同一位置
}
int PushQueue(Queue& q, MinHeapNode e)//结点e进队
{
if ((q.rear + 1) % MAXQ == q.front)//判断队是否为满
{
cout << "队列空间已满,无法进行下一步求解,可能得不到最优值!\n";
return 0;
}
else//可进队
{
q.rear = (q.rear + 1) % MAXQ;
q.Q[q.rear] = e;
return 1;
}
}
int PopQueue(Queue& q, MinHeapNode& e)//结点e出队
{
if (EmptyQueue(q))//调用判空函数
return 0;
else
{
q.front = (q.front + 1) % MAXQ;
e = q.Q[q.front];
return 1;
}
}
解法二:回溯法
测试截图:
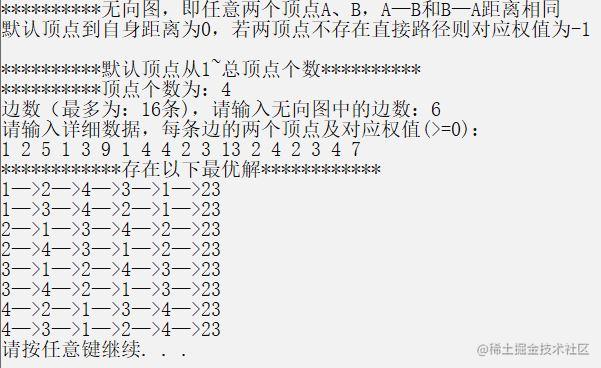

代码:
using namespace std;
int** InitMap(int N);//初始化无向图
void CreateMap(int **map);//编辑无向图
void swap(int arr[], int i, int j);//交换值
void Backtrack(int arr[], int k, int ** distance, int** path);
int M = 1;//最多有M条路径
int N;//顶点个数
int Min = 1000;//最短路线对应的距离
int num = 0;//解的个数
int sum = 0;//当前路径累加距离
int main()
{
cout << "**********无向图,即任意两个顶点A、B,A—B和B—A距离相同\n";
cout << "默认顶点到自身距离为0,若两顶点不存在直接路径则对应权值为-1\n\n";
cout << "**********默认顶点从1~总顶点个数**********\n";
cout << "**********顶点个数为:";
cin >> N;
int** Map = InitMap(N);
CreateMap(Map);
int* arr = new int[N];
for (int i = 0; i < N; i++)//初始化结点
{
arr[i] = i + 1;
}
for (int i = 1; i <= N; i++)//最多可能解个数为N!
{
M *= i;
}
int** path = new int* [M];
for (int i = 0; i < M; i++)//开辟存储解向量的空间
{
path[i] = new int[N + 1];
}
Backtrack(arr, 0, Map, path);//回溯求解最优路径所有解
if (num == 0)
{
cout << "不存在回路,即所给信息无法联通所有顶点!\n";
}
else
{
cout << "************存在以下最优解************\n";
for (int i = 0; i < num; i++)
{
for (int j = 0; j <= N; j++)
{
cout << path[i][j] << "—>";
}
cout << Min << endl;
}
}
system("pause");
return 0;
}
int** InitMap(int N)//初始化地图
{
int** map = new int* [N];
for (int i = 0; i < N; i++)
{
map[i] = new int[N];
for (int j = 0; j < N; j++)
{
if (i == j)
map[i][j] = 0;
else
map[i][j] = -1;
}
}
return map;
}
void CreateMap(int** map)//确定地图信息
{
int anum;
int sV, eV, seW;//边起始点,边终点,边权值
cout << "边数(最多为:" << N * N << "条),请输入无向图中的边数:";
cin >> anum;
cout << "请输入详细数据,每条边的两个顶点及对应权值(>=0):\n";
for (int k = 1; k <= anum; k++)
{
cin >> sV >> eV >> seW;
map[sV-1][eV-1] = seW;
map[eV-1][sV-1] = seW;
}
}
void swap(int arr[], int i, int j)//交换值
{
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
void Backtrack(int arr[], int k, int ** distance, int** path)//回溯求解最优路径所有解
{
if (k == N)//到达叶子结点
{
int w;
w = distance[arr[N - 1] - 1][arr[0] - 1]; //加上从路线终点—起点的权值,成环,回到出发点
if (w == -1)
{
return;
}
sum += w;
if (sum < Min)
{
Min = sum;//更新最小距离
num = 1;
for (int j = 0; j < N; j++)//重新存储最优路径,第一个解
path[num - 1][j] = arr[j];
path[num - 1][N] = arr[0];//终点—起点
}
else
if (sum == Min)//存储第i个解
{
num++;
for (int j = 0; j < N; j++)
path[num - 1][j] = arr[j];
path[num - 1][N] = arr[0];
}
else//sum > Min该解不满足条件,舍去
{
;//
}
sum -= distance[arr[N - 1] - 1][arr[0] - 1];//减去从路线终点—起点的权值,回溯
}
else
{
//生成当前k节点的所有孩子节点
for (int i = k; i < N; i++)
{
swap(arr, k, i);//当前k位置的元素和后边所有元素交换
int w = 0;
if (k == 0)
{
w = 0;//从根出发,还未选择任何一条路径,故w=0
}
else
w=distance[arr[k - 1] - 1][arr[k] - 1];//记录父结点到本结点的权值,后续回溯需要减去
if (w == -1)
{
swap(arr, k, i);//回溯到父节点,交换回来,因为生成新的孩子是基于父节点进行元素的交换
continue;
}
else
{
sum += w;//(起始点)arr[0]—arr[k](当前结点)的路线累加距离
if (sum > Min)//到本结点的累加距离已经大于目前最小值,由于未知量及对应系数ai>0,故再深度搜索sum只可能更大,故回溯
{
sum -= w;//回溯减去父结点到本结点的权值
swap(arr, k, i);//回溯到父节点,交换回来,因为生成新的孩子是基于父节点进行元素的交换
continue;
}
else
{
Backtrack(arr, k + 1, distance, path);//遍历k的一个孩子
sum -= w; //回溯减去父结点到本结点的权值
swap(arr, k, i);//回溯到父节点,交换回来,因为生成新的孩子是基于父节点进行元素的交换
}
}
}
}
}





 小红书公司福利 636人发布
小红书公司福利 636人发布