2054. 两个最好的不重叠活动

给你一个下标从 0 开始的二维整数数组 events ，其中 events[i] = [startTimei, endTimei, valuei] 。第 i 个活动开始于 startTime[i] ，结束于 endTime[i] ，如果你参加这个活动，那么你可以得到价值value[i]。你最多可以参加两个时间不重叠活动，使得它们的价值之和最大。请你返回价值之和的最大值。

注意:活动的开始时间和结束时间是包括在活动时间内的，也就是说，你不能参加两个活动且它们之一的开始时间等于另一个活动的结束时间。更具体的，如果你参加一个活动，且结束时间为 t ，那么下一个活动必须在 t + 1 或之后的时间开始。

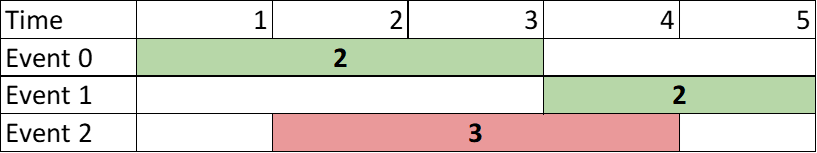
思路：

这个其实是一个比较典型的优先队列的贪心问题，可以先按活动开始的时间进行一个升序排序。遍历一遍，那么怎么选择第二个活动，要使得第二个活动与第一个活动不会重叠，所以第二个活动的开始时间一定要一定要大于第一个活动的结束时间。我们可以用一个小根堆，存下每一个活动的结束时间和活动的价值，不满足条件就pop掉，在所有情况中取一个最大值。

由于至多可以选两个活动，我们可以对活动排序，枚举其中一个活动的价值并求出其余不重叠活动的最大价值，二者相加的最大值即为答案。为了方便统计另一个活动的最大价值，我们可以对活动排序，有两种排序策略：

按开始时间排序

按结束时间排序

如果按开始时间排序，那么对于一个活动而言，结束时间小于该活动开始时间的活动必然不会与该活动重叠，因此我们可以用一个优先队列（小根堆）存储活动的结束时间和价值，这样就能在遍历活动的同时，不断从堆顶弹出小于当前活动开始时间的活动，并维护这些活动的最大价值。

如果按结束时间排序，如果是从前往后扫描活动，对于每个活动，我们需要知道小于该活动开始时间的所有活动的最大价值。但是开始时间不是有序的，最大价值不好维护。如果是从后往前扫描活动就可以做，做法同上，用大根堆存储活动的开始时间和价值。

优先队列：

priority_queue 默认的是大根堆

小根堆

 //降序，小顶堆
 priority_queue <int,vector<int>,greater<int> > q;

大根堆

 //降序队列，大顶堆
 priority_queue <int,vector<int>,less<int> >q;

代码：

class Solution {
public:
    typedef pair<int, int> PII;
    int maxTwoEvents(vector<vector<int>>& events) {
        int pre_max = INT_MIN, res = INT_MIN;
        sort(events.begin(), events.end());
        priority_queue<PII, vector<PII>, greater<PII>> q;//小根堆
        for (auto& x : events) {
            int end = x[1], val = x[2];
            q.push({end, val});
        }

        for (int i = 0; i < events.size(); i++) {
            int start = events[i][0], val = events[i][2];
            while (q.size() && q.top().first < start) {
                auto x = q.top(); q.pop();
                pre_max = max(pre_max, x.second);
            }
            res = max({val, res, pre_max + val});
        }
        return res;
    }
};