<span>020-红黑树(一)</span>

1、红黑树是什么？红黑树（英语：Red–black tree）是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。它是在1972年由鲁道夫·贝尔发明的，他称之为"对称二叉B树"，它现代的名字是在Leo J. Guibas和Robert Sedgewick于1978年写的一篇论文中获得的。它是复杂的，但它的操作有着良好的最坏情况运行时间，并且在实践中是高效的：它可以在 $\text{[math]}$ 时间内做查找，插入和删除，这里的 $n$

##################################################

###################################################################################################

###########################################################################################

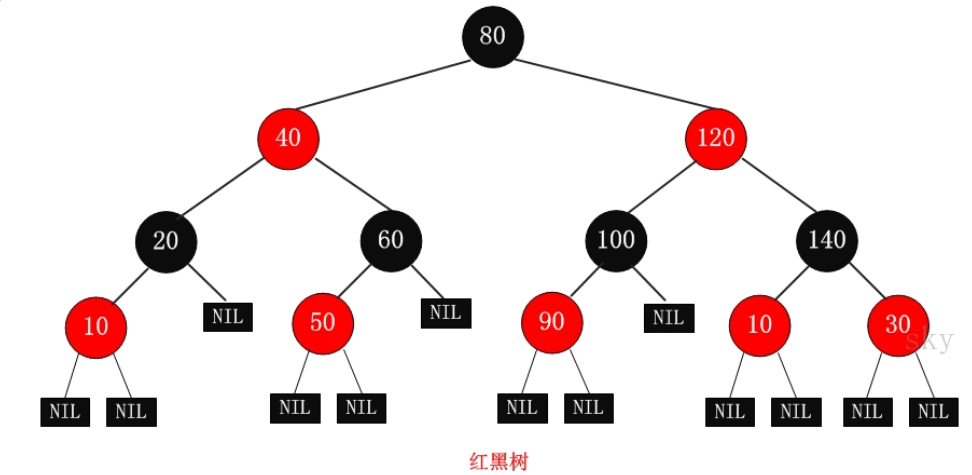
2、红黑树性质：

（1）每个结点要么是红的要么是黑的。

（2）根结点是黑的。

（3）每个叶结点（叶结点即指树尾端NIL指针或NULL结点）都是黑的。

（4）如果一个结点是红的，那么它的两个儿子都是黑的。从每个根到节点的路径上不会有两个连续的红色节点，但黑色节点是可以连续的。

（5）对于任意结点而言，其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。

总结：首先全局地看这棵树是不是只有红黑两种颜色；然后看这棵树的首尾是否全部都是黑色；再看所有的红色节点的左右子节点是否全是黑色；最后看任何节点到叶节点的所有路径是否包含相同数量的黑色节点。

3、为什么从根到叶子的最长的可能路径不多于最短的可能路径的两倍长？这些性质确保了红黑树的关键特性，结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。为什么这些性质确保了这个结果？注意到性质4导致了路径不能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点，最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点，这就表明了没有路径能多于任何其他路径的两倍长。那么对于从一个节点到其叶子节点的一条最长的路径一定是红黑交错的，那么最短路径一定是纯黑色的节点。

4、为什么使用"nil叶子"或"空（null）叶子"？在很多树数据结构的表示中，一个节点有可能只有一个子节点，而叶子节点包含数据。用这种范例表示红黑树是可能的，但是这会改变一些性质并使算法复杂。为此，本文中我们使用"nil叶子"或"空（null）叶子"。这些节点在绘图中经常被省略，导致了这些树好像同上述原则相矛盾，而实际上不是这样。与此有关的结论是所有节点都有两个子节点，尽管其中的一个或两个可能是空叶子。显然这里的叶子节点不是平常我们所说的叶子节点，如图标有NIL的为叶子节点，为什么不按常规出牌，因为按一般的叶子节点也行，但会使算法更复杂；

5、一棵含有x个节点的红黑树的高度f(x)满足不等关系：f(x) <= 2log(x+1)。

下面通过"数学归纳法"开始论证高度为h的红黑树，它的包含的内节点个数至少为 2bh(x)-1个"。
(01) 当树的高度h=0时，
内节点个数是0，bh(x) 为0，2bh(x)-1 也为 0。显然，原命题成立。
(02) 当h>0，且树的高度为 h-1 时，它包含的节点个数至少为 2bh(x)-1-1。这个是根据(01)推断出来的！
下面，由树的高度为 h-1 的已知条件推出“树的高度为 h 时，它所包含的节点树为 2bh(x)-1”。
当树的高度为 h 时，对于节点x(x为根节点)，其黑高度为bh(x)。对于节点x的左右子树，它们黑高度为 bh(x) 或者 bh(x)-1。
根据(02)的已知条件，我们已知 "x的左右子树，即高度为 h-1 的节点，它包含的节点至少为 2bh(x)-1-1 个"；
所以，节点x所包含的节点至少为 ( 2bh(x)-1-1 ) + ( 2bh(x)-1-1 ) + 1 = 2^bh(x)-1。即节点x所包含的节点至少为 2bh(x)-1。
因此，原命题成立。
由(01)、(02)得出，"高度为h的红黑树，它的包含的内节点个数至少为 2^bh(x)-1个"。
因此，“一棵含有n个节点的红黑树的高度至多为2log(n+1)”。