题解 | 信息学奥赛一本通 - 玩具装箱
E-玩具装箱_Part5.6 动态规划-斜率优化动态规划
https://ac.nowcoder.com/acm/contest/976/E
斜率优化DP
前置姿势
1. 单调队列,DP,以及单调队列优化DP
单调队列用来维护一个滑动区间的最大值,因为最多滑动不超过2n次,复杂度O(n).
P1886 滑动窗口是单调队列的模板题。
在线性DP很常用
P3957 跳房子 就是一道经典的单调队列优化动归...
(当时在考场上遇到这道题毫无头绪,现在却变成了简单题....想起来感慨很深啊...
设为到第
的花费,依次遍历
因为每个点是由一个区间转移过来的,而这个区间随着i的右移也右移,所以满足单调队列优化的条件,优化后可达到
P3572 [POI2014]PTA-Little Bird 与上道题基本一样...
2.一次函数
初中基本知识不谈
正文
这里有一个经典的问题
有一个长度为n的正整数序列,要求划分成若干段,每一段的代价为这段的和的平方+m,求划分序列的最小代价
考虑m=0,显然划分越多次越好,直接划成n段
但是有了m,划分多一段,代价就会多m,划分成n段是不划算的
先考虑的DP做法
设为原序列前缀和,
为划分前k个数最小代价,显然有
对于每一个,枚举断点
即可,时间复杂度
斜率优化要对上面这个式子进行优化
首先复读一遍式子
用完全平方公式展开
发现怎么取值,
都一定不变
移项,得
(取一个k,使得
最小)
将上面的式子转为一次函数
令
有
那么即为一条过
,斜率为
的直线,在y轴上的截距,因为
和
都是常量,所以当
最小,
即最小
那么对于每个点i,前面就有个断点,我们要在这
个点钟找到一个点,使得截距最小(也就是
最小)
再公式化地表述 就是有一条过,斜率为
的直线,截距为
,找一个点
使得截距最小
如果有三个点表示横坐标,且
在直线
的上方,那么B肯定不是最优决策

红色线为最优决策,蓝色线为选B时的决策
发现选B永远不如选A或C好(截距较大、注意截距可以为负数)
那么所有的有可能对答案有贡献的点,会形成一个下凸壳
(下凸壳就是对于任意三点(按横坐标排序),
不在
与
的连线上方)
类比于单调队列,我们每次加入一个可能可以转移的状态,就可以删掉一些无用的状态
我们发现,我们每次的,即横坐标,是单调上升的(因为
是正整数序列的前缀和),所以我们加入的决策点一个比一个偏右
这就类似于单调队列,下面模拟一下删点的过程
这是我们原来的图,红色为新加的点

连线,发现我们倒数第二个点不满足下凸壳,删去
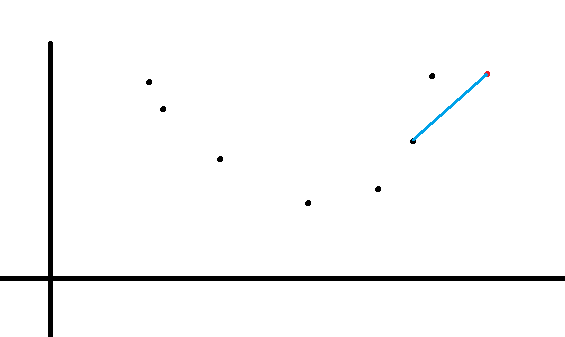
继续连线

发现下一个点也不满足下凸壳,删去


最后连一次线,发现满足

最后的形状

另外,我们可以证明,若第个点满足下凸壳,则
这些点全部满足下凸壳。
我们发现这个过程和单调队列几乎完 全 一 致,类似于单调队列,这个过程也可以用deque来维护,每个点至多进队一次,出队一次,这样扫过去的复杂度是的
以上就是加点的过程,接下来我们来看如何找到最小截距
我们发现,在这道题中我们加入的点的横坐标和直线的斜率都是递增的
再重新看一下我们的任务吧...
有一条过,斜率为
的直线,截距为
,找一个点
使得截距最小
接下来我们要找一个点使得截距最小
我们的方法是把队首弹出直至队首两个点的斜率大于等于,此时队首就是最优决策点
按上面的步骤做即可
其实这个找最优决策点的过程,类似于线性规划
玩具装箱
回到本题,先计算出前缀和
那么有
枚举断点,得到一个n方的状态转移方程,时间复杂度不正确
考虑斜率优化,令
得到式子
展开,移项
令,发现是一个可以斜率优化的式子,线性规划即可
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<string>
#include<cstdio>
#include<vector>
#include<queue>
#include<cmath>
#include<queue>
#include<map>
#include<set>
using namespace std;
typedef double db;
typedef long long ll;
inline int read() {
int res=0,fh=1;
char ch=getchar();
while((ch>'9'||ch<'0')&&ch!='-')ch=getchar();
if(ch=='-')fh=-1,ch=getchar();
while(ch>='0'&&ch<='9')res=res*10+ch-'0',ch=getchar();
return fh*res;
}
const int maxn=100010;
int n,l;
db sum[maxn],f[maxn];
int hd,tl,q[maxn];
inline db a(int i){return sum[i]+i;}
inline db b(int i){return a(i)+l+1;}
inline db X(int i){return b(i);}
inline db Y(int i){return f[i]+b(i)*b(i);}
inline db slope(int i,int j){
return (Y(i)-Y(j))/(X(i)-X(j));
}
int main()
{
n=read(),l=read();
for(int i=1;i<=n;i++){
scanf("%lf",&sum[i]);
sum[i]+=sum[i-1];
}
hd=tl=1;
for(int i=1;i<=n;i++){
while(hd<tl&&slope(q[hd],q[hd+1])<2*a(i)) hd++;
f[i]=f[q[hd]]+(a(i)-b(q[hd]))*(a(i)-b(q[hd]));
while(hd<tl&&slope(i,q[tl-1])<slope(q[tl-1],q[tl])) --tl;
q[++tl]=i;
}
printf("%.0lf\n",f[n]);
return 0;
}  查看16道真题和解析
查看16道真题和解析


