SGU 110 Dungeon(立体几何)

Description:

The mission of space explorers found on planet M the vast dungeon. One of the dungeon halls is fill with the bright spheres. The explorers find out that the light rays reflect from the surface of the spheres according the ordinary law (the incidence angle is equal to the reflectance angle, the incidence ray, the reflected ray and the perpendicular to the sphere surface lay in the one plane). The ancient legend says that if the light ray will reflect from the spheres in the proper order, than the door to the room with very precious ancient knowledge will open. You are not to guess the right sequence; your task is much simpler. You are given the positions and the radii of the spheres, the place where the laser shot was made and the direction of light propagation. And you must find out the sequence in which the light will be reflected from the spheres.

Input:

The first line of input contains the single integer n (1≤n≤50) - the amount of the spheres. The next n lines contain the coordinates and the radii of the spheres xi, yi, zi, ri (the integer numbers less or equal to 10000 by absolute value). The last line contains 6 real numbers - the coordinates of two points. The first one gives the coordinates of the place of laser shot, and the second gives the direction in which it was made (the second point is the point on the ray). The starting point of the ray lies strictly outside of any sphere.

Output:

Your program must output the sequence of sphere numbers (spheres are numbers from 1 as they was given in input), from which the light ray was reflected. If the ray will reflect more the 10 times, than you must output first 10, then a space and the word ‘etc.’ (without quotes). Notice: if the light ray goes at a tangent to the sphere you must assume that the ray was reflected by the sphere.

Sample Input:

1
0 0 2 1
0 0 0 0 0 1

Sample Output:

1

Sample Input:

2
0 0 2 1
0 0 -2 1
0 0 0 0 0 100

Sample Output:

1 2 1 2 1 2 1 2 1 2 etc.

题目链接

在空间内有 $n$n 个球和一条射线，射线照射到球面上会发生反射（相切也算反射），求射线路径中依次发生反射的球体编号（超过10次反射仅输出10次反射的球体编号和etc.）

从题目数据范围看对于每次的射线可以暴力枚举每个球判断其是否相交，其中相交切交点最近的球为反射球，再求出反射射线重复上述过程即可

首先需要判断射线是否与球体相交，显然射线经球反射后的反射线一定在射线的起点、秋心和射线与球的交点三点确定的平面上，这样就可以把立体几何先转化到平面几何上然后再继续分析

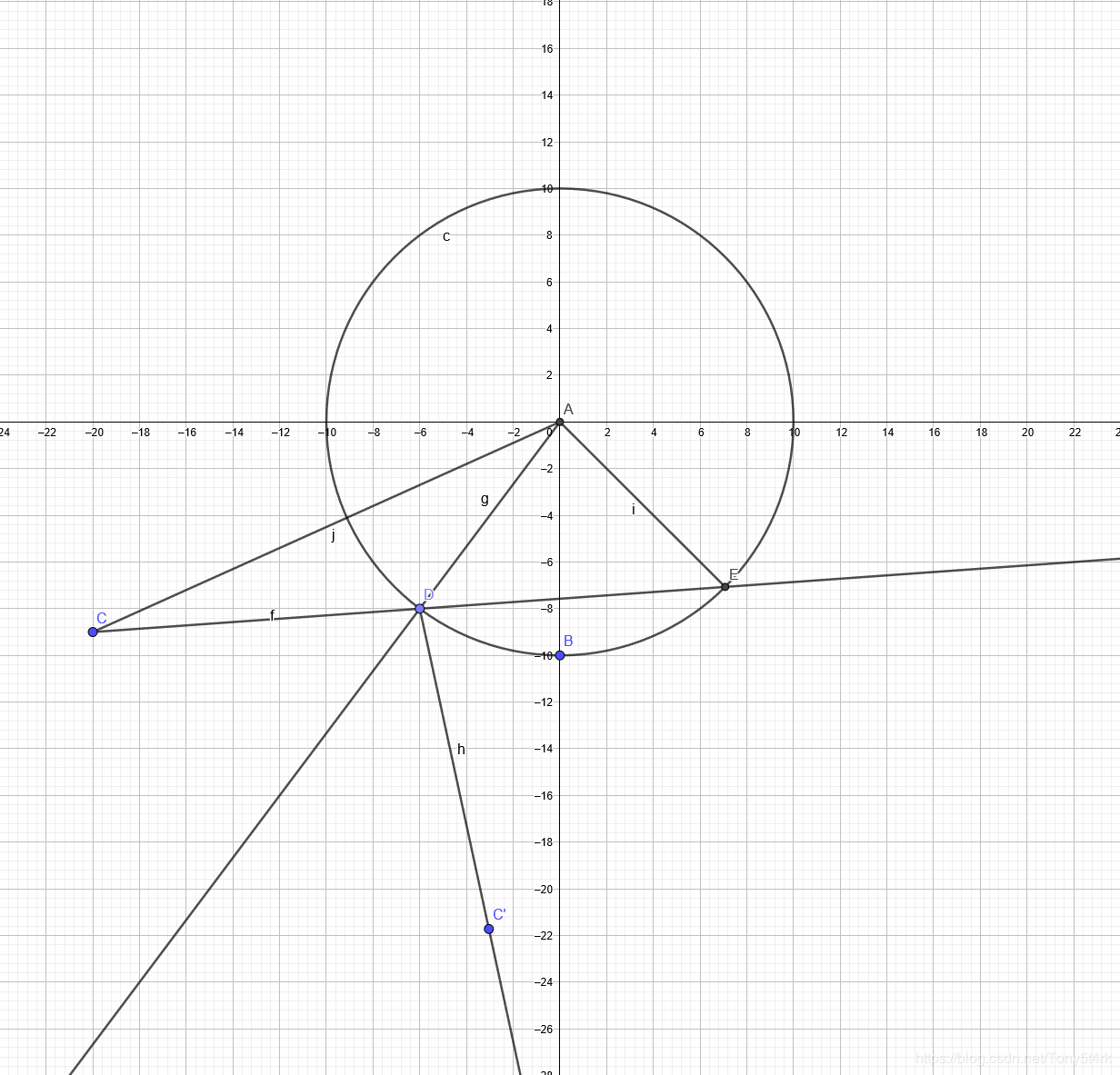
若射线为图中 $CD$CD ，球为 $\odot A$⊙A ，射线与球的交点为 $D、F$D、F ，反射线为 $D{C}^{\prime }$DC′ （ $C^{\prime }$C′ 为 $C$C 关于法线 $AD$AD 的对称点 ）

我们只讨论射线与球的一个交点 $D$D ， $E$E 暂且不讨论

根据向量的关系可得 $\overrightarrow{DA}=\overrightarrow{CA}-\overrightarrow{CD}$DA =CA −CD 而 $\mid \overrightarrow{DA}\mid =r$∣DA ∣=r （ $r$r 是球 $A$A 的半径）

假设 $\mid \overrightarrow{CD}\mid =l$∣CD ∣=l , $\overrightarrow{CD}$CD 的方向向量为 $\overrightarrow{dir}$dir ， $CD=l\times \overrightarrow{dir}$CD=l×dir

联立得 $\mid \overrightarrow{CA}-l\times \overrightarrow{dir}\mid =R$∣CA −l×dir ∣=R 其中 $l$l 为变量

这样我们就得到了一个关于 $l$l 的一元二次方程，方程化简到最后为
${\overrightarrow{AC}}^2+2l\overrightarrow{AC}\overrightarrow{dir}+l^2{\overrightarrow{dir}}^2=r^2$AC 2+2lAC dir +l2dir 2=r2
移项得
$l^2{\overrightarrow{dir}}^2+2l\overrightarrow{AC}\overrightarrow{dir}+{\overrightarrow{AC}}^2{r}^2=0$l2dir 2+2lAC dir +AC 2r2=0
设 $a={\overrightarrow{dir}}^2,b=2\overrightarrow{AC}\overrightarrow{dir},c={\overrightarrow{AC}}^2$a=dir 2,b=2AC dir ,c=AC 2 ，根据根的判别式 $\Delta =b^2-4ac$Δ=b2−4ac 就可以判断射线所在的直线是否与球体相交，若相交则继续利用求根公式求出两解 $\frac{-b\pm \sqrt{\Delta }}{2a}$2a−b±Δ ​​ ，取最小解（显然图中 $\mid \overrightarrow{CD}\mid \&lt;\mid \overrightarrow{CE}\mid$∣CD ∣<∣CE ∣ ），若最小解为负数则射线所在直线与球体相交但射线不与球体相交（球体在射线反向），若最小解为 $0$0 则射线与球体相切，若最小解为整数则射线与球体相交

判断完是否相交就需要求出射线经球体反射后的反射线了

因为此题的射线是用两点（射线起点与射线上另一点）表示，所以反射线的起点可以用入射线与球体的交点表示，而另一反射线上的点利用入射线起点对于法线的对称点表示就可以啦

AC代码:

#include <bits/stdc++.h>
using namespace std;
typedef double db;
const int maxn = 1e2 + 5;
const db inf = 1e20;
const db eps = 1e-9;

int Sgn(db Key) {return fabs(Key) < eps ? 0 : (Key < 0 ? -1 : 1);}
int Cmp(db Key1, db Key2) {return Sgn(Key1 - Key2);}
struct Point {db X, Y, Z;};
typedef Point Vector;
struct Ray {Point Origin; Vector Dir;};
Vector operator - (Vector Key1, Vector Key2) {return (Vector){Key1.X - Key2.X, Key1.Y - Key2.Y, Key1.Z - Key2.Z};}
Vector operator + (Vector Key1, Vector Key2) {return (Vector){Key1.X + Key2.X, Key1.Y + Key2.Y, Key1.Z + Key2.Z};}
db operator * (Vector Key1, Vector Key2) {return Key1.X * Key2.X + Key1.Y * Key2.Y + Key1.Z * Key2.Z;}
db GetLen(Vector Key) {return sqrt(Key * Key);}
db GetLen2(Vector Key) {return Key * Key;}
db operator ^ (Vector Key1, Vector Key2) {return GetLen((Vector){Key1.Y * Key2.Z - Key1.Z * Key2.Y, Key1.Z * Key2.X - Key1.X * Key2.Z, Key1.X * Key2.Y - Key1.Y * Key2.X});}
Vector operator * (Vector Key1, db Key2) {return (Vector){Key1.X * Key2, Key1.Y * Key2, Key1.Z * Key2};}
Vector operator / (Vector Key1, db Key2) {return (Vector){Key1.X / Key2, Key1.Y / Key2, Key1.Z / Key2};}
db DisPointToPoiont(Point Key1, Point Key2) {return GetLen(Key2 - Key1);}
struct Sphere {Point Center; db Radius;};

bool IsRayInterSphere(Ray Key1, Sphere Key2, db &Dis) {
    db A = Key1.Dir * Key1.Dir;
    db B = (Key1.Origin - Key2.Center) * Key1.Dir * 2.0;
    db C = ((Key1.Origin - Key2.Center) * (Key1.Origin - Key2.Center)) - (Key2.Radius * Key2.Radius);
    db Delta = B * B - 4.0 * A * C;
    if (Sgn(Delta) < 0) return false;
    db X1 = (-B - sqrt(Delta)) / (2.0 * A), X2 = (-B + sqrt(Delta)) / (2.0 * A);
    if (Cmp(X1, X2) > 0) swap(X1, X2);
    if (Sgn(X1) <= 0) return false;
    Dis = X1;
    return true;
}

void Reflect(Ray &Key1, Sphere Key2, db Dis) {
    Point Pos = Key1.Origin + (Key1.Dir * Dis);
    Vector Temp = Key2.Center + (((Pos - Key2.Center) * ((Pos - Key2.Center) * (Key1.Origin - Key2.Center))) / GetLen2(Pos - Key2.Center));
    Key1.Dir = Temp * 2.0 - Key1.Origin - Pos; Key1.Origin = Pos;
}

int N;
Sphere spheres[maxn];
Ray Cur;
int Last;

int Solve() {
    db MinDis = inf; int Ans = -1;
    for (int i = 1; i <= N; ++i) {
        db Dis = inf;
        if (i == Last) continue;
        if (!IsRayInterSphere(Cur, spheres[i], Dis)) continue;
        if (Cmp(Dis, MinDis) < 0) {
            Ans = i;
            MinDis = Dis;
        }
    }
    if (Ans == -1) return -1;
    Last = Ans;
    Reflect(Cur, spheres[Ans], MinDis);
    return Ans;
}

int main(int argc, char *argv[]) {
    scanf("%d", &N);
    for (int i = 1; i <= N; ++i) scanf("%lf%lf%lf%lf", &spheres[i].Center.X, &spheres[i].Center.Y, &spheres[i].Center.Z, &spheres[i].Radius);
    scanf("%lf%lf%lf", &Cur.Origin.X, &Cur.Origin.Y, &Cur.Origin.Z);
    scanf("%lf%lf%lf", &Cur.Dir.X, &Cur.Dir.Y, &Cur.Dir.Z);
    Cur.Dir = Cur.Dir - Cur.Origin;
    for (int i = 0, Ans; i < 11; ++i) {
        Ans = Solve();
        if (Ans == -1) break;
        else if (i == 10) printf("etc.");
        else printf("%d ", Ans);
    }
    printf("\n");
    return 0;
}