误差补偿模型——世界坐标系，视觉坐标系，图像坐标系和装配坐标系之间的转换

就像来自遥远宇宙的一束光，不知道它从哪里来，也不知道它到哪里去，从我们头上掠过，波澜不惊。

误差来源

视觉测量误差主要来源有：图像采集误差，相机安装误差，运动平台误差。其中高精度的CCD传感器与图像采集卡的误差微乎其微可以忽略；相机坐标系如果与水平面不共面或共面但是存在夹角都会引入误差；三维运动平台的几何误差的垂直度问题将导致图像处理中的圆心提取和图像拼接，误差需要补偿。

坐标系转换

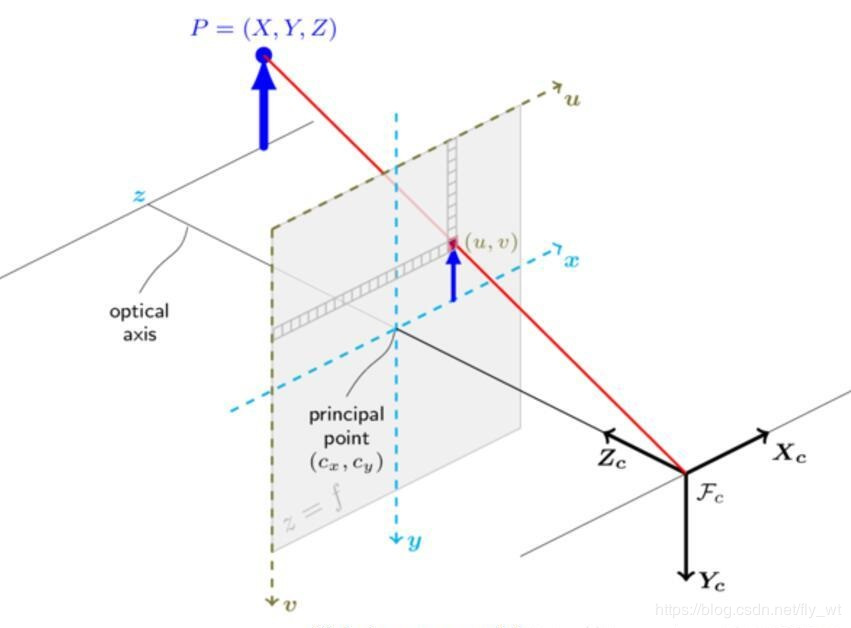
1. 图像坐标系
   
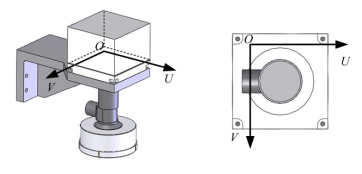
   图像坐标系建立在CCD传感器的面上如上图。
2. 视觉坐标系
   
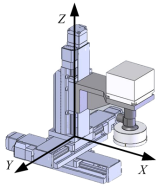
3. 装配作业坐标系
   与视觉坐标系建系相同
   
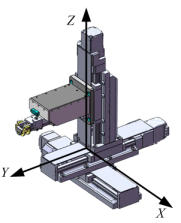
4. 世界坐标系
   世界坐标系是空间绝对坐标系，选取视觉坐标为世界坐标系即可

转换

各坐标系的空间位置如图所示，三维运动平台中X轴和Y轴滑台不垂直，YV0和YC0为实际的Y轴滑台运动方向。图像坐标系UOV与世界坐标系XWOYW之间的夹角为θ，以世界坐标系XW轴为基准，图像U轴向世界坐标系Y轴正方向偏转为正，反之为负。视觉测量模块三维运动平台X轴与YV0轴滑台之间的夹角为α。世界坐标系和装配作业坐标系XCOYC之间的夹角为φ，以世界坐标系X轴为基准，装配作业坐标系X轴向世界坐标系Y轴正方向偏转为正，反之为负。装配作业模块三维运动平台X轴与YC0轴滑台之间夹角为β。

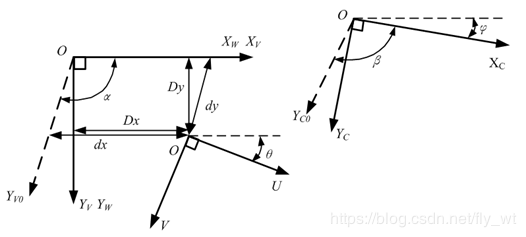
根据坐标系之间的坐标转换关系建立误差补偿模型，以图像中一点为例，分别将其从图像坐标系装换到世界坐标系和装配作业坐标系中。
首先完成由图像坐标系向世界坐标系的转换，设图像中一点（u，v），其在世界坐标系中的坐标为（x，y），由于图像坐标系单位为像素，世界坐标系单位为微米，单位转换关系为：
$\begin{array}{}\text{(1)}& P=\{\begin{array}{c}{u}_0=u\times S_x\\ v_0=v\times S_y\end{array}\end{array}$P={u0​=u×Sx​v0​=v×Sy​​(1)
相应的矩阵形式 $M_s$Ms​为：
$\begin{array}{}\text{(2)}& M_s=\left[\begin{array}{ccc}{S}_x& 0& 0\\ 0& S_y& 0\\ 0& 0& 1\end{array}\right]\end{array}$Ms​=⎣⎡​Sx​00​0Sy​0​001​⎦⎤​(2)

图像坐标系和世界坐标系坐标轴之间存在夹角θ，需对图像坐标系进行旋转，旋转矩阵 $M_R$MR​为：
$\begin{array}{}\text{(3)}& M_R=\left[\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]\end{array}$MR​=⎣⎡​cosθsinθ0​−sinθcosθ0​001​⎦⎤​(3)
采集过程中相机会变换采集位置，应该对图像坐标系原点和世界坐标系原点之间的距离进行补偿，需要进行平移变换，相应的平移变换矩阵 $M_T$MT​为：
$\begin{array}{}\text{(4)}& M_T=\left[\begin{array}{ccc}1& 0& D_x\\ 0& 1& D_y\\ 0& 0& 1\end{array}\right]\end{array}$MT​=⎣⎡​100​010​Dx​Dy​1​⎦⎤​(4)
图像坐标系原点在世界坐标系中的坐标值（Dx，Dy）无法直接获取，从图5.4可知，相机在三维运动平台中XY向滑台位移分别为dx和dy，经计算得出此时相机在世界坐标系的坐标（Dx，Dy），计算公式为：
$\begin{array}{}\text{(5)}& \{\begin{array}{c}{D}_x=d_x-d_y\times sin(\alpha -90^o)\\ D_y=d_y\times cos(\alpha -90^o)\end{array}\end{array}${Dx​=dx​−dy​×sin(α−90o)Dy​=dy​×cos(α−90o)​(5)
图像中一点（u，v）转换为世界坐标系一点（x，y）的误差补偿模型表达式为：
$\begin{array}{}\text{(6)}& \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& d_x-d_y\times sin(\alpha -90^o)\\ 0& 1& d_y\times cos(\alpha -90^o)\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}{S}_x& 0& 0\\ 0& S_y& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]\end{array}$⎣⎡​xy1​⎦⎤​=⎣⎡​100​010​dx​−dy​×sin(α−90o)dy​×cos(α−90o)1​⎦⎤​⎣⎡​cosθsinθ0​−sinθcosθ0​001​⎦⎤​⎣⎡​Sx​00​0Sy​0​001​⎦⎤​⎣⎡​uv1​⎦⎤​(6)
得到零件在世界坐标系中的坐标后，装配作业模块夹持壳体完成对正。由于世界坐标系和装配作业坐标系之间存在夹角，并且装配作业模块XY滑台不垂直，需要进行误差补偿。
装配过程仅需获取两个零件圆心的相对位置，不要求零件的绝对位置。可直接建立相对位置转换的误差补偿模型。设两零件在世界坐标系中的距离为（ΔX，ΔY），转换到装配作业坐标系后坐标为（ΔXC，ΔYC）。
首先对世界坐标系进行旋转补偿夹角φ，旋转矩阵 $M_R$MR​为：
$\begin{array}{}\text{(7)}& M_R=\left[\begin{array}{ccc}cos\phi & sin\phi & 0\\ -sin\phi & cos\phi & 0\\ 0& 0& 1\end{array}\right]\end{array}$MR​=⎣⎡​cosφ−sinφ0​sinφcosφ0​001​⎦⎤​(7)
旋转变换之后得到两个圆心在装配作业坐标系中的坐标差，由于装配作业模块XY向滑台不垂直，需要计算出XY滑台应该补偿的实际距离，转换矩阵 $M_D$MD​为：
$\begin{array}{}\text{(8)}& M_D=\left[\begin{array}{ccc}1& tan(\beta -90^o)& 0\\ 0& sec(\beta -90^o)& 0\\ 0& 0& 1\end{array}\right]\end{array}$MD​=⎣⎡​100​tan(β−90o)sec(β−90o)0​001​⎦⎤​(8)
零件圆心世界坐标系中的坐标差转换到装配作业坐标系中，并计算出实际的XY滑台补偿位移量（ΔXC0，ΔYC0）误差补偿模型的矩阵表达式为：
$\begin{array}{}\text{(9)}& \left[\begin{array}{c}\Delta X_{CO}\\ \Delta Y_{CO}\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& tan(\beta -90^o)& 0\\ 0& sec(\beta -90^o)& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}cos\phi & sin\phi & 0\\ -sin\phi & cos\phi & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}\Delta X\\ \Delta Y\\ 1\end{array}\right]\end{array}$⎣⎡​ΔXCO​ΔYCO​1​⎦⎤​=⎣⎡​100​tan(β−90o)sec(β−90o)0​001​⎦⎤​⎣⎡​cosφ−sinφ0​sinφcosφ0​001​⎦⎤​⎣⎡​ΔXΔY1​⎦⎤​(9)
终于敲完了，latex确实很好用，矩阵书写很方便，坚持用Markdown来写博客！