一、贝叶斯公式的秘密

在计算概率中，常常可以看见贝叶斯公式的应用。那么为什么要应用贝叶斯公式呢？因为它可以帮我们根据先验的概率，来计算在先验基础上，后面事件发生的概率。如果先验事件变化了，后面事件发生的概率也会随之而变化，体现了事物否定之否定的发展规律。

二、贝叶斯公式是什么？

贝叶斯公式如下所示，H是假设，或者基本概率，或者可以称之为先验事件，~H为假设不成立事件。E是指新的证据，或者是在假设的条件下，新出来事件。 公式最终要得出来的结论就是在新证据补充进来之后，原假设的概率变为多少。 说个大白话，举两个例子。 1、我之前以为中午吃面条的概率是90%，不过现在我妈买了饺子皮，那么现在中午吃面条的概率变为了多少？ 2、我之前以为中概股基金从2022年1月1日至2023年1月1日价格上涨的概率是80%，那么P（H）为80%，基金下跌的话P( ~ H)为20%，不过现在它已经跌了50%，在基金上涨的前提下，基金下跌50%的概率为P（E|H),在基金下跌的前提下，基金下跌50%的概率为P（E|~H）， 那么中概股基金上涨的概率变为了多少？

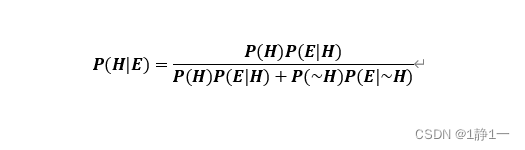
将例子2中的概率值代入上图的公式中，即可计算新的概率。

三、贝叶斯公式的内在逻辑

贝叶斯公式的内在逻辑就是基于假设，以及新的证据，来修正假设的概率。 比如说在人群中得病的概率为1%,不得病的概率为99%。现在某人查出得病了，那么检查报告的准确性是多少？ 这时候就需要思考，在得病的前提下，检查出来是真的生病的概率是多少，比如80%，因为检测结果有时候也不准。以及在不得病前提下，检查出来生病的概率，假如是30%。 上面这个思考方式就是，在假设的正反两方面推现有的结论的概率，相当于是对现状的一个较为全面的分析。 最后计算查出来得病，真得病的概率，就是1%*80%/(1%*80%+99% * 30% ) = 2.6% 检测结果不靠谱啊，那么换一种高级的检测方法。此时某人得病的概率就变为2.6%了，因为这个人已经属于经过一次检测的人啦。 总之，贝叶斯公式是在现实中很常用的一种思考问题的方式，基于整体情况做假设，然后新的证据加入，打破整体情况的平衡。我们需要思考，假设成立，导致新证据的概率，以及假设不成立，导致新证据的概率。因为无法得知新证据是假设成立还是不成立产生的，所以每种情况都要考虑到。然后基于上述4个概率来做出新的假设。 可能有的人会想P(H|E)是以及如何计算？这个就需要翻看条件概率的内容啦。本文不再赘述。