C++精通之路:红黑树的应用(模拟实现map/set)
@[toc]
> 很多小伙伴为了刷题发愁
> 今天为大家推荐一款刷题神奇哦:[刷题面试神器牛客](https://www.nowcoder.com/link/pc_csdncpt_xfh_sf)
> 各大互联网大厂面试真题。从基础到入阶乃至原理刨析类面试题 应有尽有,赶快来装备自己吧!助你面试稳操胜券,solo全场面试官
# 一:红黑树的迭代器
* 需要注意的是:
>1. 迭代器本质上是指针的一个封装的类,其底层就是指针;好处是可以方便遍历,是数据结构的底层实现与用户透明
>2. 对于string,vector,list等容器,其本身的结构上是比较简单的,迭代器的实现也很简单;但是对于二叉树结构的红黑树来说需要考虑很多的问题
## 1.begin()与end()
> STL明确规定,begin()与end()代表的是一段前闭后开的区间
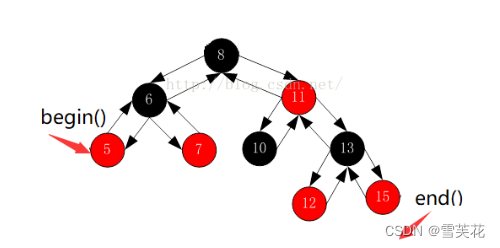
> 对红黑树进行中序遍历后,可以得到一个有序的序列,因此begin()可以放在红黑树中最小节点(即最左侧节点)的位置,end()放在最大节点(最右侧节点)的下一个位置即nullptr
* 如图:
## 2.operator++()与operator--()
* ++逻辑的实现:
1. 因为红黑树的中序是有序的,所以++是找到该节点在中序中的下一个节点
2. 因为中序是左中右,所以我们可以分为右子树存在和不存在来讨论下一个节点是谁
> 1. 当右子树存在时,右子树的最左节点即是下一个节点
> 2. 当右子树不存在时,我们需要向上寻找,因为中序是左中右的,所以该子树已经被遍历完了,则++操作后应该在该结点的祖先结点中找到孩子不在父亲右的祖先
* --的逻辑是一样的
### 代码实现:
* operator++()
```cpp
Self& operator++()
{
if (_node->_right)//右子节点存在
{
//找到右子树中最左节点
Node* cur = _node->_right;
while (cur->_left)
{
cur = cur->_left;
}
_node = cur;
}
else//右子节点不存在,向上找
{
Node* cur = _node;//记录走过的节点
Node* parent = _node->_parent;
while (parent && parent->_right == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
```
* operator--():
```cpp
Self& operator--()
{
if (_node->_left)//左子节点存在
{
//找左子树中的最右节点
Node* cur = _node->_left;
while (cur->_right)
{
cur = cur->_right;
}
_node = cur;
}
else//左子节点不存在
{
Node* cur = _node;
Node* parent = _node->_parent;
while (parent && parent->_left == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
```
## 反向迭代器适配器
> 因为反向迭代器与正向迭代器在原理实现中是相同的,只是方向反了而已
> 所以我们可以用正向迭代器来封装出反向迭代器,在正向迭代器的基础上,对其接口进行封装达到反向迭代器的效果
* 正向迭代器实现代码:
```cpp
template<class T, class Ref, class Ptr>
struct _TreeIterator
{
//声明类型,便于反向迭代器对类型的提取
typedef Ref reference;
typedef Ptr pointer;
typedef RBTreeNode<T> Node;
typedef _TreeIterator<T, Ref, Ptr> Self;
Node* _node;
_TreeIterator(Node* node)
:_node(node)
{}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &_node->_data;
}
bool operator==(const Self& it)const
{
return _node == it._node;
}
bool operator!= (const Self& it)const
{
return _node != it._node;
}
Self& operator++()
{
if (_node->_right)
{
Node* cur = _node->_right;
while (cur->_left)
{
cur = cur->_left;
}
_node = cur;
}
else
{
Node* cur = _node;
Node* parent = _node->_parent;
while (parent && parent->_right == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Self& operator--()
{
if (_node->_left)
{
Node* cur = _node->_left;
while (cur->_right)
{
cur = cur->_right;
}
_node = cur;
}
else
{
Node* cur = _node;
Node* parent = _node->_parent;
while (parent && parent->_left == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
};
```
* 反向迭代器实现代码:
```cpp
//适配器构造反向迭代器
template<class Iterator>
struct ReverseIterator
{
//类型未实例化,无法取出里面的类型,此时需要使用typename:告诉编译器等实例化后再到类里面找对应的类型
typedef typename Iterator::reference Ref;
typedef typename Iterator::pointer Ptr;
typedef ReverseIterator<Iterator> Self;
Iterator _it;
ReverseIterator(Iterator it)
:_it(it)
{}
//在正向迭代器接口上进行封装复用
Ref operator*()
{
return *_it;
}
Ptr operator->()
{
return _it.operator->();
}
bool operator==(const Self& it)const
{
return it._it==_it;
}
bool operator!= (const Self& it)const//两个const
{
return _it != it._it;
}
Self& operator++()
{
--_it;
return *this;
}
Self& operator--()
{
++_it;
return *this;
}
};
```
# 二:改造红黑树来模拟实现map/set
> 因为set是K模型的容器,而map是KV模型的容器.所以要用红黑树来模拟实现这两个容器,需要添加一些东西使得其能适配两者,添加和改变的东西如下:
## 1. 节点的改变:
>对于红黑树的节点我们需要节点对于set来说储存key,对于map来说储存key-value键值对,所以这里我们就直接让节点类型的阈值类型为T,用来控制储存类型
* 代码的实现:
```cpp
template<class T>
struct RBTreeNode
{
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;//T可以是key也可以是pair<K,V>
Colour _col;
RBTreeNode(const T& data)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
, _col(RED)
{}
};
```
## 2. 主体的改变
```cpp
template<class K, class T>
class RBTree
{
typedef RBTreeNode<T> Node;
public:
//.......
private:
Node* _root;
};
```
> K是用来比较的类型,T是用来存储的类型
* 这里就体现了对map和set的兼容。
> * 当为map时,传进来的T为pirpair<key,value>
> * 当为set时,传进来的T为K
* 达到了存储不同数据类型的目的
## 3. 添加仿函数来适配数据间的比较
> 在删除添加时,我们要进行节点中数据的比较,
> 当为map时,pirpair<key,value>与Kl类型无法比较时,这里就需要仿函数来帮助我们适配
* 对于不同容器我们需要不同的仿函数类型,由此在红黑树的模板列表中还需要一个模板类型参数,灵活控制传入的仿函数类型
> 仿函数的本质是创造一个类,通过operator()的重载来实现的,与函数重载类似,但在模板内,就只能使用仿函数来实现了。
* 红黑树框架:
```cpp
template<class K, class T, class KeyOfT>
class RBTree
{
typedef RBTreeNode<T> Node;
public:
//...
private:
Node* _root;
};
```
* map实现框架:
```cpp
namespace cole
{
template<class K, class V>
class map
{
struct MapOfKey
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
public:
//...
private:
RBTree<K, pair<const K, V>, MapOfKey> _t;
};
}
```
* set实现框架:
```cpp
namespace cole
{
template<class K>
class set
{
struct SetOfKey
{
const K& operator()(const K& key)
{
return key;
}
};
public:
//...
private:
RBTree<K, K, SetOfKey> _t;
};
}
```
* 仿函数使用示例:
Node* Find(const K& key)
{
KeyOfT kot;
Node* cur = _root;
while (cur)
{
if (kot(cur->_kv.first) > key)
{
cur = cur->_left;
}
else if (kot(cur->_kv.first) < key)
{
cur = cur->_right;
}
else
{
return cur;
}
}
return nullptr;
}
# 三:红黑树的封装与适配
* 代码:
```cpp
//颜***r /> enum Colour
{
RED,
BLACK,
};
template<class T>
struct RBTreeNode
{
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;//T可以是key也可以是pair<K,V>
Colour _col;
RBTreeNode(const T& data)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
, _col(RED)
{}
};
template<class K, class T, class KeyOfT>
class RBTree
{
typedef RBTreeNode<T> Node;
public:
typedef _TreeIterator<T, T&, T*> iterator;
typedef _TreeIterator<T,const T&, const T*> const_iterator;
typedef ReverseIterator<iterator> reverse_iterator;
typedef ReverseIterator<const_iterator> reverse_const_iterator;
RBTree()
:_root(nullptr)
{}
~RBTree()
{
_Destory(_root);
}
iterator begin()
{
Node* cur = _root;
while (cur&&cur->_left)
{
cur = cur->_left;
}
return iterator(cur);
}
reverse_iterator rbegin()
{
Node* cur = _root;
while (cur&&cur->_right)
{
cur = cur->_right;
}
return reverse_iterator(iterator(cur));
}
reverse_iterator rend()
{
return reverse_iterator(iterator(nullptr));
}
iterator end()
{
return iterator(nullptr);
}
Node* Find(const K& key)
{
KeyOfT kot;
Node* cur = _root;
while (cur)
{
if (kot(cur->_kv.first) > key)
{
cur = cur->_left;
}
else if (kot(cur->_kv.first) < key)
{
cur = cur->_right;
}
else
{
return cur;
}
}
return nullptr;
}
pair<iterator, bool> Insert(const T& data)
{
//空树的情况
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;
return make_pair(iterator(_root), true);
}
KeyOfT kot;
//查找位置插入节点
Node* cur = _root, * parent = _root;
while (cur)
{
if (kot(cur->_data) > kot(data))
{
parent = cur;
cur = cur->_left;
}
else if (kot(cur->_data) < kot(data))
{
parent = cur;
cur = cur->_right;
}
else
{
return make_pair(iterator(cur), false);
}
}
//创建链接节点
cur = new Node(data);
Node* newnode = cur;
if (kot(parent->_data) > kot(data))
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
//父节点存在且为红,则需要调整(不能存在连续的红色节点)
while (parent && parent->_col == RED)
{
//此时当前节点一定有祖父节点
Node* granparent = parent->_parent;
//具体调整情况主要看叔叔节点
//分左右讨论
if (parent == granparent->_left)
{
Node* uncle = granparent->_right;
//情况1:叔叔节点存在且为红
if (uncle && uncle->_col == RED)
{
//修改颜色,继续向上检查
granparent->_col = RED;
parent->_col = uncle->_col = BLACK;
cur = granparent;
parent = cur->_parent;
}
else//情况2和3:叔叔节点不存在 或者存在且为黑
{
//单旋(三代节点为斜线)+变***r /> if (cur == parent->_left)
{
RotateR(granparent);
granparent->_col = RED;
parent->_col = BLACK;
}
else//双旋(三代节点为折线)+变***r /> {
RotateL(parent);
RotateR(granparent);
cur->_col = BLACK;
granparent->_col = RED;
}
//旋转后不需再向上调整了
break;
}
}
else//parent=grandparent->right
{
Node* uncle = granparent->_left;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
granparent->_col = RED;
cur = granparent;
parent = cur->_parent;
}
else
{
if (cur == parent->_right)
{
RotateL(granparent);
parent->_col = BLACK;
granparent->_col = RED;
}
else
{
RotateR(parent);
RotateL(granparent);
cur->_col = BLACK;
granparent->_col = RED;
}
break;
}
}
}
//确保根节点为黑
_root->_col = BLACK;
return make_pair(iterator(newnode), true);
}
bool IsRBTree()
{
if (_root == nullptr)
{
return true;
}
if (_root->_col == RED)
{
cout << "根节点为红色" << endl;
return false;
}
int Blacknum = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
Blacknum++;
cur = cur->_left;
}
int i = 0;
return _IsRBTree(_root, Blacknum, i);
}
private:
void _Destory(Node*& root)
{
if (root == nullptr)
return;
_Destory(root->_left);
_Destory(root->_right);
delete root;
root = nullptr;
}
bool _IsRBTree(Node* root, int blacknum, int count)
{
if (root == nullptr)
{
if (blacknum == count)
return true;
cout << "各路径上黑色节点个数不同" << endl;
return false;
}
if (root->_col == RED && root->_parent->_col == RED)
{
cout << "存在连续红色节点" << endl;
return false;
}
if (root->_col == BLACK)
count++;
return _IsRBTree(root->_left, blacknum, count) && _IsRBTree(root->_right, blacknum, count);
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* parentP = parent->_parent;
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
subR->_left = parent;
parent->_parent = subR;
if (parent == _root)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
subR->_parent = parentP;
if (parentP->_left == parent)
{
parentP->_left = subR;
}
else
{
parentP->_right = subR;
}
}
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* parentP = parent->_parent;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
subL->_right = parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
subL->_parent = parentP;
if (parentP->_left == parent)
{
parentP->_left = subL;
}
else
{
parentP->_right = subL;
}
}
}
private:
Node* _root;
};
```
# 四:map的封装和模拟实现
* 代码:
```cpp
namespace ymhh
{
template<class K, class V>
class map
{
struct MapOfKey
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
public:
typedef typename RBTree<K, pair<const K, V>, MapOfKey>::iterator iterator;
typedef typename RBTree<K, pair<const K, V>, MapOfKey>::reverse_iterator reverse_iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}
pair<iterator, bool> insert(const pair<const K, V>& kv)
{
return _t.Insert(kv);
}
V& operator[](const K& key)
{
pair<iterator, bool> ret = insert(make_pair(key, V()));
return ret.first->second;
}
iterator find(const K& key)
{
return _t.Find(key);
}
private:
RBTree<K, pair<const K, V>, MapOfKey> _t;
};
}
```
# 五: set的封装和模拟实现
* 代码:
```cpp
namespace ymhh
{
template<class K>
class set
{
struct SetOfKey
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef typename RBTree<K,K, SetOfKey>::iterator iterator;
typedef typename RBTree<K,K, SetOfKey>::reverse_iterator reverse_iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}
pair<iterator, bool> insert(const K& key)
{
return _t.Insert(key);
}
iterator find(const K& key)
{
return _t.Find(key);
}
private:
RBTree<K, K, SetOfKey> _t;
};
}
```
# 总结
> 因为红黑树的增删查改都是O(logN),所以用红黑树实现的map/set的增删查改也是O(logN),是个非常优秀的容器
> 很多小伙伴为了刷题发愁
> 今天为大家推荐一款刷题神奇哦:[刷题面试神器牛客](https://www.nowcoder.com/link/pc_csdncpt_xfh_sf)
> 各大互联网大厂面试真题。从基础到入阶乃至原理刨析类面试题 应有尽有,赶快来装备自己吧!助你面试稳操胜券,solo全场面试官
# 一:红黑树的迭代器
* 需要注意的是:
>1. 迭代器本质上是指针的一个封装的类,其底层就是指针;好处是可以方便遍历,是数据结构的底层实现与用户透明
>2. 对于string,vector,list等容器,其本身的结构上是比较简单的,迭代器的实现也很简单;但是对于二叉树结构的红黑树来说需要考虑很多的问题
## 1.begin()与end()
> STL明确规定,begin()与end()代表的是一段前闭后开的区间
> 对红黑树进行中序遍历后,可以得到一个有序的序列,因此begin()可以放在红黑树中最小节点(即最左侧节点)的位置,end()放在最大节点(最右侧节点)的下一个位置即nullptr
* 如图:

## 2.operator++()与operator--()
* ++逻辑的实现:
1. 因为红黑树的中序是有序的,所以++是找到该节点在中序中的下一个节点
2. 因为中序是左中右,所以我们可以分为右子树存在和不存在来讨论下一个节点是谁
> 1. 当右子树存在时,右子树的最左节点即是下一个节点
> 2. 当右子树不存在时,我们需要向上寻找,因为中序是左中右的,所以该子树已经被遍历完了,则++操作后应该在该结点的祖先结点中找到孩子不在父亲右的祖先
* --的逻辑是一样的
### 代码实现:
* operator++()
```cpp
Self& operator++()
{
if (_node->_right)//右子节点存在
{
//找到右子树中最左节点
Node* cur = _node->_right;
while (cur->_left)
{
cur = cur->_left;
}
_node = cur;
}
else//右子节点不存在,向上找
{
Node* cur = _node;//记录走过的节点
Node* parent = _node->_parent;
while (parent && parent->_right == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
```
* operator--():
```cpp
Self& operator--()
{
if (_node->_left)//左子节点存在
{
//找左子树中的最右节点
Node* cur = _node->_left;
while (cur->_right)
{
cur = cur->_right;
}
_node = cur;
}
else//左子节点不存在
{
Node* cur = _node;
Node* parent = _node->_parent;
while (parent && parent->_left == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
```
## 反向迭代器适配器
> 因为反向迭代器与正向迭代器在原理实现中是相同的,只是方向反了而已
> 所以我们可以用正向迭代器来封装出反向迭代器,在正向迭代器的基础上,对其接口进行封装达到反向迭代器的效果
* 正向迭代器实现代码:
```cpp
template<class T, class Ref, class Ptr>
struct _TreeIterator
{
//声明类型,便于反向迭代器对类型的提取
typedef Ref reference;
typedef Ptr pointer;
typedef RBTreeNode<T> Node;
typedef _TreeIterator<T, Ref, Ptr> Self;
Node* _node;
_TreeIterator(Node* node)
:_node(node)
{}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &_node->_data;
}
bool operator==(const Self& it)const
{
return _node == it._node;
}
bool operator!= (const Self& it)const
{
return _node != it._node;
}
Self& operator++()
{
if (_node->_right)
{
Node* cur = _node->_right;
while (cur->_left)
{
cur = cur->_left;
}
_node = cur;
}
else
{
Node* cur = _node;
Node* parent = _node->_parent;
while (parent && parent->_right == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Self& operator--()
{
if (_node->_left)
{
Node* cur = _node->_left;
while (cur->_right)
{
cur = cur->_right;
}
_node = cur;
}
else
{
Node* cur = _node;
Node* parent = _node->_parent;
while (parent && parent->_left == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
};
```
* 反向迭代器实现代码:
```cpp
//适配器构造反向迭代器
template<class Iterator>
struct ReverseIterator
{
//类型未实例化,无法取出里面的类型,此时需要使用typename:告诉编译器等实例化后再到类里面找对应的类型
typedef typename Iterator::reference Ref;
typedef typename Iterator::pointer Ptr;
typedef ReverseIterator<Iterator> Self;
Iterator _it;
ReverseIterator(Iterator it)
:_it(it)
{}
//在正向迭代器接口上进行封装复用
Ref operator*()
{
return *_it;
}
Ptr operator->()
{
return _it.operator->();
}
bool operator==(const Self& it)const
{
return it._it==_it;
}
bool operator!= (const Self& it)const//两个const
{
return _it != it._it;
}
Self& operator++()
{
--_it;
return *this;
}
Self& operator--()
{
++_it;
return *this;
}
};
```
# 二:改造红黑树来模拟实现map/set
> 因为set是K模型的容器,而map是KV模型的容器.所以要用红黑树来模拟实现这两个容器,需要添加一些东西使得其能适配两者,添加和改变的东西如下:
## 1. 节点的改变:
>对于红黑树的节点我们需要节点对于set来说储存key,对于map来说储存key-value键值对,所以这里我们就直接让节点类型的阈值类型为T,用来控制储存类型
* 代码的实现:
```cpp
template<class T>
struct RBTreeNode
{
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;//T可以是key也可以是pair<K,V>
Colour _col;
RBTreeNode(const T& data)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
, _col(RED)
{}
};
```
## 2. 主体的改变
```cpp
template<class K, class T>
class RBTree
{
typedef RBTreeNode<T> Node;
public:
//.......
private:
Node* _root;
};
```
> K是用来比较的类型,T是用来存储的类型
* 这里就体现了对map和set的兼容。
> * 当为map时,传进来的T为pirpair<key,value>
> * 当为set时,传进来的T为K
* 达到了存储不同数据类型的目的
## 3. 添加仿函数来适配数据间的比较
> 在删除添加时,我们要进行节点中数据的比较,
> 当为map时,pirpair<key,value>与Kl类型无法比较时,这里就需要仿函数来帮助我们适配
* 对于不同容器我们需要不同的仿函数类型,由此在红黑树的模板列表中还需要一个模板类型参数,灵活控制传入的仿函数类型
> 仿函数的本质是创造一个类,通过operator()的重载来实现的,与函数重载类似,但在模板内,就只能使用仿函数来实现了。
* 红黑树框架:
```cpp
template<class K, class T, class KeyOfT>
class RBTree
{
typedef RBTreeNode<T> Node;
public:
//...
private:
Node* _root;
};
```
* map实现框架:
```cpp
namespace cole
{
template<class K, class V>
class map
{
struct MapOfKey
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
public:
//...
private:
RBTree<K, pair<const K, V>, MapOfKey> _t;
};
}
```
* set实现框架:
```cpp
namespace cole
{
template<class K>
class set
{
struct SetOfKey
{
const K& operator()(const K& key)
{
return key;
}
};
public:
//...
private:
RBTree<K, K, SetOfKey> _t;
};
}
```
* 仿函数使用示例:
Node* Find(const K& key)
{
KeyOfT kot;
Node* cur = _root;
while (cur)
{
if (kot(cur->_kv.first) > key)
{
cur = cur->_left;
}
else if (kot(cur->_kv.first) < key)
{
cur = cur->_right;
}
else
{
return cur;
}
}
return nullptr;
}
# 三:红黑树的封装与适配
* 代码:
```cpp
//颜***r /> enum Colour
{
RED,
BLACK,
};
template<class T>
struct RBTreeNode
{
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;//T可以是key也可以是pair<K,V>
Colour _col;
RBTreeNode(const T& data)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
, _col(RED)
{}
};
template<class K, class T, class KeyOfT>
class RBTree
{
typedef RBTreeNode<T> Node;
public:
typedef _TreeIterator<T, T&, T*> iterator;
typedef _TreeIterator<T,const T&, const T*> const_iterator;
typedef ReverseIterator<iterator> reverse_iterator;
typedef ReverseIterator<const_iterator> reverse_const_iterator;
RBTree()
:_root(nullptr)
{}
~RBTree()
{
_Destory(_root);
}
iterator begin()
{
Node* cur = _root;
while (cur&&cur->_left)
{
cur = cur->_left;
}
return iterator(cur);
}
reverse_iterator rbegin()
{
Node* cur = _root;
while (cur&&cur->_right)
{
cur = cur->_right;
}
return reverse_iterator(iterator(cur));
}
reverse_iterator rend()
{
return reverse_iterator(iterator(nullptr));
}
iterator end()
{
return iterator(nullptr);
}
Node* Find(const K& key)
{
KeyOfT kot;
Node* cur = _root;
while (cur)
{
if (kot(cur->_kv.first) > key)
{
cur = cur->_left;
}
else if (kot(cur->_kv.first) < key)
{
cur = cur->_right;
}
else
{
return cur;
}
}
return nullptr;
}
pair<iterator, bool> Insert(const T& data)
{
//空树的情况
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;
return make_pair(iterator(_root), true);
}
KeyOfT kot;
//查找位置插入节点
Node* cur = _root, * parent = _root;
while (cur)
{
if (kot(cur->_data) > kot(data))
{
parent = cur;
cur = cur->_left;
}
else if (kot(cur->_data) < kot(data))
{
parent = cur;
cur = cur->_right;
}
else
{
return make_pair(iterator(cur), false);
}
}
//创建链接节点
cur = new Node(data);
Node* newnode = cur;
if (kot(parent->_data) > kot(data))
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
//父节点存在且为红,则需要调整(不能存在连续的红色节点)
while (parent && parent->_col == RED)
{
//此时当前节点一定有祖父节点
Node* granparent = parent->_parent;
//具体调整情况主要看叔叔节点
//分左右讨论
if (parent == granparent->_left)
{
Node* uncle = granparent->_right;
//情况1:叔叔节点存在且为红
if (uncle && uncle->_col == RED)
{
//修改颜色,继续向上检查
granparent->_col = RED;
parent->_col = uncle->_col = BLACK;
cur = granparent;
parent = cur->_parent;
}
else//情况2和3:叔叔节点不存在 或者存在且为黑
{
//单旋(三代节点为斜线)+变***r /> if (cur == parent->_left)
{
RotateR(granparent);
granparent->_col = RED;
parent->_col = BLACK;
}
else//双旋(三代节点为折线)+变***r /> {
RotateL(parent);
RotateR(granparent);
cur->_col = BLACK;
granparent->_col = RED;
}
//旋转后不需再向上调整了
break;
}
}
else//parent=grandparent->right
{
Node* uncle = granparent->_left;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
granparent->_col = RED;
cur = granparent;
parent = cur->_parent;
}
else
{
if (cur == parent->_right)
{
RotateL(granparent);
parent->_col = BLACK;
granparent->_col = RED;
}
else
{
RotateR(parent);
RotateL(granparent);
cur->_col = BLACK;
granparent->_col = RED;
}
break;
}
}
}
//确保根节点为黑
_root->_col = BLACK;
return make_pair(iterator(newnode), true);
}
bool IsRBTree()
{
if (_root == nullptr)
{
return true;
}
if (_root->_col == RED)
{
cout << "根节点为红色" << endl;
return false;
}
int Blacknum = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
Blacknum++;
cur = cur->_left;
}
int i = 0;
return _IsRBTree(_root, Blacknum, i);
}
private:
void _Destory(Node*& root)
{
if (root == nullptr)
return;
_Destory(root->_left);
_Destory(root->_right);
delete root;
root = nullptr;
}
bool _IsRBTree(Node* root, int blacknum, int count)
{
if (root == nullptr)
{
if (blacknum == count)
return true;
cout << "各路径上黑色节点个数不同" << endl;
return false;
}
if (root->_col == RED && root->_parent->_col == RED)
{
cout << "存在连续红色节点" << endl;
return false;
}
if (root->_col == BLACK)
count++;
return _IsRBTree(root->_left, blacknum, count) && _IsRBTree(root->_right, blacknum, count);
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* parentP = parent->_parent;
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
subR->_left = parent;
parent->_parent = subR;
if (parent == _root)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
subR->_parent = parentP;
if (parentP->_left == parent)
{
parentP->_left = subR;
}
else
{
parentP->_right = subR;
}
}
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* parentP = parent->_parent;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
subL->_right = parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
subL->_parent = parentP;
if (parentP->_left == parent)
{
parentP->_left = subL;
}
else
{
parentP->_right = subL;
}
}
}
private:
Node* _root;
};
```
# 四:map的封装和模拟实现
* 代码:
```cpp
namespace ymhh
{
template<class K, class V>
class map
{
struct MapOfKey
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
public:
typedef typename RBTree<K, pair<const K, V>, MapOfKey>::iterator iterator;
typedef typename RBTree<K, pair<const K, V>, MapOfKey>::reverse_iterator reverse_iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}
pair<iterator, bool> insert(const pair<const K, V>& kv)
{
return _t.Insert(kv);
}
V& operator[](const K& key)
{
pair<iterator, bool> ret = insert(make_pair(key, V()));
return ret.first->second;
}
iterator find(const K& key)
{
return _t.Find(key);
}
private:
RBTree<K, pair<const K, V>, MapOfKey> _t;
};
}
```
# 五: set的封装和模拟实现
* 代码:
```cpp
namespace ymhh
{
template<class K>
class set
{
struct SetOfKey
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef typename RBTree<K,K, SetOfKey>::iterator iterator;
typedef typename RBTree<K,K, SetOfKey>::reverse_iterator reverse_iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}
pair<iterator, bool> insert(const K& key)
{
return _t.Insert(key);
}
iterator find(const K& key)
{
return _t.Find(key);
}
private:
RBTree<K, K, SetOfKey> _t;
};
}
```
# 总结
> 因为红黑树的增删查改都是O(logN),所以用红黑树实现的map/set的增删查改也是O(logN),是个非常优秀的容器

 查看13道真题和解析
查看13道真题和解析

