“蔚来杯“2022牛客暑期多校训练营1 补题题解（A、C、D、G、I、J）

Villages: Landlines

https://ac.nowcoder.com/acm/contest/33186/A

A Villages: Landlines

比赛时候写出来的，但是自己最初对题意的理解很不到位，想的很复杂，多亏队友想出来的思路，以后还要继续多练请添加图片描述

请添加图片描述

#include<bits/stdc++.h>

using namespace std;

#define int long long

const int N = 2e5 + 10;

struct edge{
	int t, R, l, r;
	bool operator<(const edge &y) const{
		return l < y.l;
	}
}ed[N];

int n, m;
int ans;

signed main()
{
	cin>>n;
	for(int i = 0; i < n; i ++ ){
		int a, b;
		scanf("%lld%lld", &ed[i].t, &ed[i].R);
		ed[i].l = ed[i].t - ed[i].R;
		ed[i].r = ed[i].t + ed[i].R;
	}
	
	sort(ed, ed + n);  //区间排序
	
	//区间合并
	int res = ed[0].r;  //记录区间右端点
	for(int i = 0; i < n; i ++ ){
	//	cout<<ed[i].l<<' '<<ed[i].r<<endl;		
		if(ed[i].l > res){  //如果前后两区间不相交
			ans += (ed[i].l - res);
			res = max(ed[i].r, res);
		}
		else if(ed[i].l <= res){  //如果两个区间相交 
			res = max(ed[i].r, res);
		}
	} 
	
	cout<<ans<<endl;
	return 0;
}

C Grab the Seat!

请添加图片描述赛后补题不得不感慨这道题思维还是比较复杂的，连带看带想带写差不多两个小时，主要思路还是借鉴大佬的，题目大概就是找出没有被覆盖的区域的点数量，观察图可以发现，被覆盖区域由两点斜线决定，斜率最大的斜线是被覆盖区域的上界，斜率最小的斜线是被覆盖区域的下界。找上界：第一行不做处理（因为第一行的点不会产生覆盖区域），从第二行开始依次遍历到第m行，对于一个新插入的点（即代表的一个直线）如果斜率大于之前的斜率那么完全可以只考虑新插入的这条直线的覆盖情况，否则这条新插入的直线可以不考虑他的影响，然后对新处理出的直线求与当前行的交点坐标，因为是整数点所以需要向上取整，即可得到对当前行的覆盖情况，对于每一行都进行同样的操作，向下的直线同理。求交点其实就是把方程：在这里插入图片描述大佬题解原地址

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

const int N = 2e5 + 10;

struct Node{
	ll x, y;
}nod[N];  //记录位置 

struct K{
	ll x, y;
	bool operator < (const K &t) const{
		return y * t.x < x * t.y;  //按斜率递增排序 
	}
};

int n, m, k, q;

void calc(){  //更新状态得出答案 
	vector<ll> minn(m + 1, n + 1);  //记录每一行最左边的被占的点 
	vector<ll> res(m + 1, n + 1);  //储存每一行和覆盖面上/下界交点 
	for(int i = 1; i <= k; i ++ ){
		minn[nod[i].y] = min(minn[nod[i].y], nod[i].x);  //找出这一行中最靠左的点的横坐标，这个点在这一行中斜率最大 
	}
	
	K a = {1, 0};
	for(ll i = 2; i <= m; i ++ ){  //处理上边界  
		a = max(a, K{minn[i], i - 1});  //a记录的值是因为这一行的最左端的被占点而被挡住的区域的上边界点，就是a记录的点和原点构成的直线就是被挡住区域的上边界
		res[i] = min(res[i], (i - 1) * a.x / a.y + ((i - 1) * a.x % a.y != 0));  //得出当先被覆盖范围的上界和当前行的交点，加号后面的((i - 1) * a.x % a.y != 0)是向上取整，带入几组数组算一下就能理解 
	}
	
	a = {1, 0};
	for(ll i = m - 1; i >= 1; i -- ){  //处理下边界 
		a = min(a, K{minn[i], i - m});  //minn[i]和i - m构成的直线的斜率等于minn[i]和m构成的直线斜率
		res[i] = min(res[i], (i - m) * a.x / a.y + ((i - m) * a.x % a.y != 0));  //更新交点，交点要是两个交线的最小值，就是这一行最左端 
	}
	
	ll ans = 0;
	for(int i = 1; i <= m; i ++ ){
		ans += res[i] - 1;
	}
	cout<<ans<<endl;
} 

int main()
{
	cin>>n>>m>>k>>q;
	for(int i = 1; i <= k; i ++ ){
		cin>>nod[i].x>>nod[i].y;  //读入被占的位置，i代表同学的id
	}
	
	while(q -- ){
		int id, x, y;
		cin>>id>>x>>y;
		//更新状态 
		nod[id].x = x;
		nod[id].y = y;
		calc();
	}
	return 0;
}

D Mocha and Railgun

比赛时候写出来的，需要考虑挺多情况，另外要注意db的精度问题和细节问题，交了15次一直没过就是有个小细节写错了，好在一直在审代码，最后时间写出来了请添加图片描述我们自己推出的结论是当Q点和O点构成的直线与直径重合时，所能覆盖到的弧长最长

官方题解：请添加图片描述

#include<bits/stdc++.h>

using namespace std;

#define pi acos(-1)
#define db double

int n, m;
int T;
db r;
db x[2], d;
db ans;
db a;  //记录圆心角

db get_dis(db x, db y){
	return sqrt(x * x + y * y);
}

int main()
{
	cin>>T;
	while(T -- ){  //OQ和AB直线重合 
		cin>>r;
		cin>>x[0]>>x[1]>>d;
		db oq = get_dis(x[0], x[1]);
		if(x[0] == 0 && x[1] == 0){  //Q点和原点重合 
			ans = asin(d / r) * r * 2.0;
		}
		else if(oq == d){  //Q点和原点不重合 
			ans = asin(2 * d / r) * r ;
		}
		else if(oq * oq + d * d == r * r){  //A、B刚好搭到圆上 
			ans = asin(d / r) * 2 * r;
		}
		else if(oq > d){
			db OB = oq - d;
			db BB1 = sqrt(r * r - OB * OB);
			db OB1x = sqrt(r * r - (oq + d) * (oq + d));
			db x = BB1 - OB1x;
			db A1B1 = sqrt(x * x + 4 * d * d);
			ans = asin(A1B1 / (2.0 * r)) * 2.0 * r;
		}
		else if(oq < d){
			db OB = d - oq;
			db a1 = acos(OB / r);
			db OA = oq + d;
			db a2 = acos(OA / r);
			db a = pi - a1 - a2;
			ans = a * r;
		}
		printf("%.7lf\n", ans);
	}
	return 0; 
}

G Lexicographical Maximum

比赛中写出来的第一题，刚开始想太简单了，后来规避了一下特殊情况就过了，通过这道题还学会了字典序，美滋滋请添加图片描述

请添加图片描述

#include<bits/stdc++.h>

using namespace std;

#define int long long

int ans;
int n;

signed main()
{
	string str;
	cin>>str;
	bool flag = true;
	for(int i = 0; i < str.length() - 1; i ++ ){
		if(str[i] != '9'){
			flag = false;
			break;
		}
	}
	
	if(str.length() == 1) cout<<str<<endl;
	else{
		if(flag){
			cout<<str<<endl;
		}
		else{
			for(int i = 1; i < str.length(); i ++ ) cout<<9;
			cout<<endl;
		}
	}
	return 0;
}

I Chiitoitsu

这道题是赛后补的，比赛时候一看没思路就放弃了，给足够时间的话其实可以冲一冲，但是比赛时间不太够，以后还是得继续练请添加图片描述

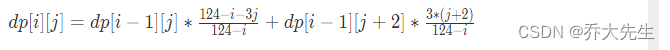
用dp解，dp[i][j]抽了i次牌，手中还有j张单牌的概率，状态转移方程如下：请添加图片描述

解释一下：一副牌总共有34*4=136张牌，除去手牌13张就是还剩123张，所以从第一次抽牌就是从（124-1）张牌中抽取想要的牌，所以分母都是124-i，前半段表示第i次抽排没有凑成对子的状态①，第i-1次抽牌，手中剩余的单牌数量为j，第i次抽牌需要和手中j张单牌匹配成对子的牌的数量是3j，牌的总数是124-i，所以抽不到理想牌的概率就是（124-i-3j）/(124-i) 后半段表示第i次抽牌凑成了对子的状态②，第i-1次抽牌，手中剩余的单牌数量为j+2（因为第i次抽牌凑成了对子，所以手中的单牌数量-2，一张是凑成的对子，一张是弃牌），第i次抽牌需要和手中j+2张单牌匹配成对子的牌的数量是3(j+2)，牌的总数是124-i，所以抽到理想牌的概率就是3（j+2）/(124-i)

算完概率之后算期望期望公式（原谅一个大二的还需要百度了才想起来(-_-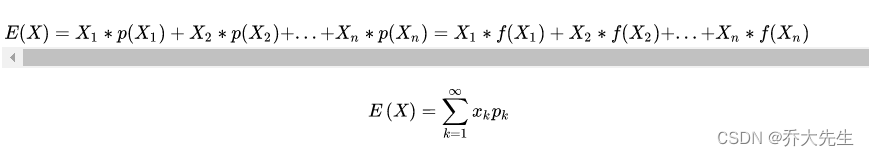）：请添加图片描述所以本题的期望公式就是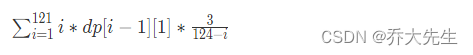：这么长的六百是为了避免这个水印盖住字emmm....... dp数组是抽了i-1次，手中还剩一张单牌的概率，i就是抽到第i次，这次胡的概率就是从现有的124-i张牌中抽3张能和手中哪一张单牌匹配成对子的牌所有该解释的基本解释完毕，下面上代码：

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

const int N = 130, M = 15, mod = 1e9 + 7;

ll dp[N][M];  //dp[i][j]表示抽了第i次，手中剩余的单牌还有j张的情况
int T, n, m;
ll op[15];
map<string, int>mp; //记录牌类对应的数量 
string str[N];

ll ksm(ll a, ll b){
	ll res = 1;
	while(b){
		if(b & 1) res = res * a % mod;
		b >>= 1;
		a = a * a % mod;
	}
	return res;
}

void init()
{
	for(int k = 1; k <= 13; k += 2){  //k代表手中单牌数量，只有1、3、5、7、9、11、13的情况 
		memset(dp, 0, sizeof dp);  //初始化清零dp数组
		dp[0][k] = 1;
		//初始化所有概率 
		for(int i = 1; i <= 121; i ++ ){  //最多抽121次牌，抽的第121次后，还剩两张牌，是一定能胡的 
			for(int j = 1; j <= 13; j += 2){  
				//i是第一维，在i-1的所有状态都初始化之后，[i-1][j+2]是已经被处理过的可用状态 
				dp[i][j] = (dp[i - 1][j + 2] * 3 * (j + 2) % mod + dp[i - 1][j] * (124 - i - 3 * j) % mod) % mod * ksm(124 - i, mod - 2) % mod; 
			}
		}
		
		ll ans = 0;  //计算期望 
		for(int i = 1; i <= 121; i ++ ){
			ans = (ans + (i * dp[i - 1][1] * 3) % mod * ksm(124 - i, mod - 2) % mod) % mod;
		} 
		op[k] = ans;  //统计初始单牌数为k的期望 
	}
}

signed main()
{
	init();  //初始化 
	cin>>T;
	for(int i = 1; i <= T; i ++ ){
		string sre;
		cin>>sre;
		int ids = 0;  //记录初始牌种类数
		mp.clear();  //清空 
		for(int i = 0; i < sre.size(); i += 2){
            str[ids].clear();
			str[ids] += sre[i];
			str[ids] += sre[i + 1];
			mp[str[ids]] ++ ;  //这种牌的数量++ 
			ids ++ ; 
		}
		int k = 0;  //记录单张牌的个数 
		for(int i = 0; i < ids; i ++ ){
          //  cout<<str[i]<<endl;
			if(mp[str[i]] == 1) k ++ ; 
		}		
       // cout<<k<<endl;
		cout<<"Case #"<<i<<": "<<op[k]<<endl;
	}
	return 0;
}

J Serval and Essay

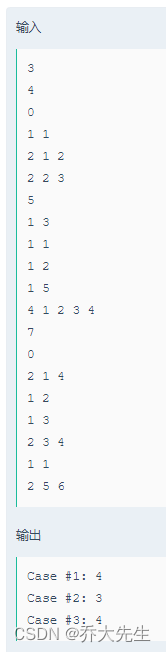请添加图片描述这道题主要复杂在理解题意，个人感觉这道题的样例解释不太好，这里再解释一下样例：输入的第一行是测试数，每组测试的第一行输入的是论点个数（图中点的个数），之后每一行的第一个数是这个论点所需要的支撑论点的数量（父节点个数），随后是支撑论点都哪些对于case1：有4个论点，第一个论点只能置为真，否则不会为真（题中所述ki=0的情况），第二个论点需要的支撑论点数量为1，需要论点1为真他才为真，第三个论点需要论点1、2为真他才为真，第四个论点需要论点2、3为真他才为真。先将论点1置为真，所以论点2为真；论点1、2为真，所以论点3为真；论点2、3为真，所以论点4为真，所以case1答案是4 对于case2：将论点1置为真，所以论点2为真；所以论点3为真，此时论点1、2、3为真，无法证明论点4或5为真，所以case2答案为3 对于case3：将论点2置为真，所以论点3为真；所以论点4为真；论点3、4为真，所以论点5为真，此时论点2、3、4、5为真，无法证明论点1、6、7为真，所以答案为4

解释完样例之后，来想一下思路。就是根据所给条件建图（想象为一张图，实际不用建图操作），将i论点所依赖的j节点（j节点可能不止一个）视为i的父节点，之后遍历所有节点，找到入度为1的节点x，用并查集操作，则所有依赖x的节点y对于x的依赖可以消除，且所有对y依赖的节点，其依赖关系可以把y换成x（把从y的入度减去，加上从x的入度，如果本身有从x入度，则这个节点的入度总数可实现-1），则依赖y节点的数量就要归并入依赖x的节点数量，之后继续找依赖关系为1（入度为1）的节点，直到不存在入度为1的节点。之后遍历所有节点，找到被依赖最多的节点，这个节点为初始黑点的话最后能染Max数量的节点，这个Max就是答案

#include<bits/stdc++.h>

using namespace std;

#define x first
#define y second

typedef pair<int, int>PII;

const int N = 2e5 + 10;

int fa[N], Size[N];  //维护并查集
int n, m;
int k[N];
set<int>from[N];  //from[i]记录推出i点需要的点
set<int>to[N];  //to[i]记录i点可以推出的点

int find(int u){  //并查集寻根函数 
	if(u != fa[u]) fa[u] = find(fa[u]);
	return fa[u];
}

void Merge(int a, int b){  //b依赖a 
	int ha = find(a), hb = find(b);
	if(ha == hb) return ;
	if(to[ha].size() < to[hb].size()) swap(ha, hb);  //将较少的集合放入大的 
	fa[hb] = ha;
	Size[ha] += Size[hb];  //由于此时只要确定了ha就能确定hb，所以所有需要依赖hb的点都可以改为需要ha的点，就是将两者数量合并
	vector<PII>tmp;  //记录所有可以入度为1的点 
	for(auto u : to[hb]){  //遍历所有依赖hb的点，现在这些点都是依赖a的(所有依赖b的点在之前的hb和b的合并过程中已经转为依赖hb，所以这里遍历的是from[hb] 
		from[u].erase(hb);  //将点u依赖hb的关系消除 
		from[u].insert(ha);  //加上点u依赖ha(可能这个关系本来就存在，set会自动去重) 
		to[ha].insert(u);  //记录ha能推出u 
		
		if(from[u].size() == 1){  //记录入度为1的点 
			tmp.push_back({ha, u});
		} 
	}
	
	for(int i = 0; i < tmp.size(); i ++ ){
		Merge(tmp[i].x, tmp[i].y);
	}
}

int main()
{
	int T;
	cin>>T;
	for(int iu = 1; iu <= T; iu ++ ){
		cin>>n;
		for(int i = 1; i <= n; i ++ ){  //清空状态记录 
			fa[i] = i;
			Size[i] = 1;
			to[i].clear();
			from[i].clear();
		}
		
		for(int i = 1; i <= n; i ++ ){
			int k;
			cin>>k;
			for(int j = 0; j < k; j ++ ){
				int a;
				cin>>a;
				from[i].insert(a);  //记录a对i的依赖关系 
				to[a].insert(i);  //记录i对a的被依赖关系 
			}
		}
		
		for(int i = 1; i <= n; i ++ ){
			if(from[i].size() == 1){
				Merge(i, *from[i].begin());
			}
		}
		int ans = 0;
		for(int i = 1; i <= n; i ++ ){
			ans = max(ans, Size[i]);
		}
		cout<<"Case #"<<iu<<": "<<ans<<endl;
	}
	return 0;
}