一文搞懂二叉搜索树

前言

大家好，我是bigsai。

前面介绍学习的大多是线性表相关的内容，把指针搞懂后其实也没有什么难度，规则相对是简单的，后面会讲解一些比较常见的数据结构，用多图的方式让大家更容易吸收。

在数据结构与算法中，树是一个比较大的家族，家族中有很多厉害的成员，这些成员有二叉树和多叉树(例如B+树等)，而二叉树的大家族中，二叉搜索树(又称二叉排序树)是最最基础的，在这基础上才能继续拓展学习AVL(二叉平衡树)、红黑树等知识。

对于二叉排序树而言，本章重点关注其实现方式以及插入、删除步骤流程，我们会手写一个二叉排序树，二叉树遍历部分的内容比较多会单独详细讲解。

什么是树

树是一种数据结构，它是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。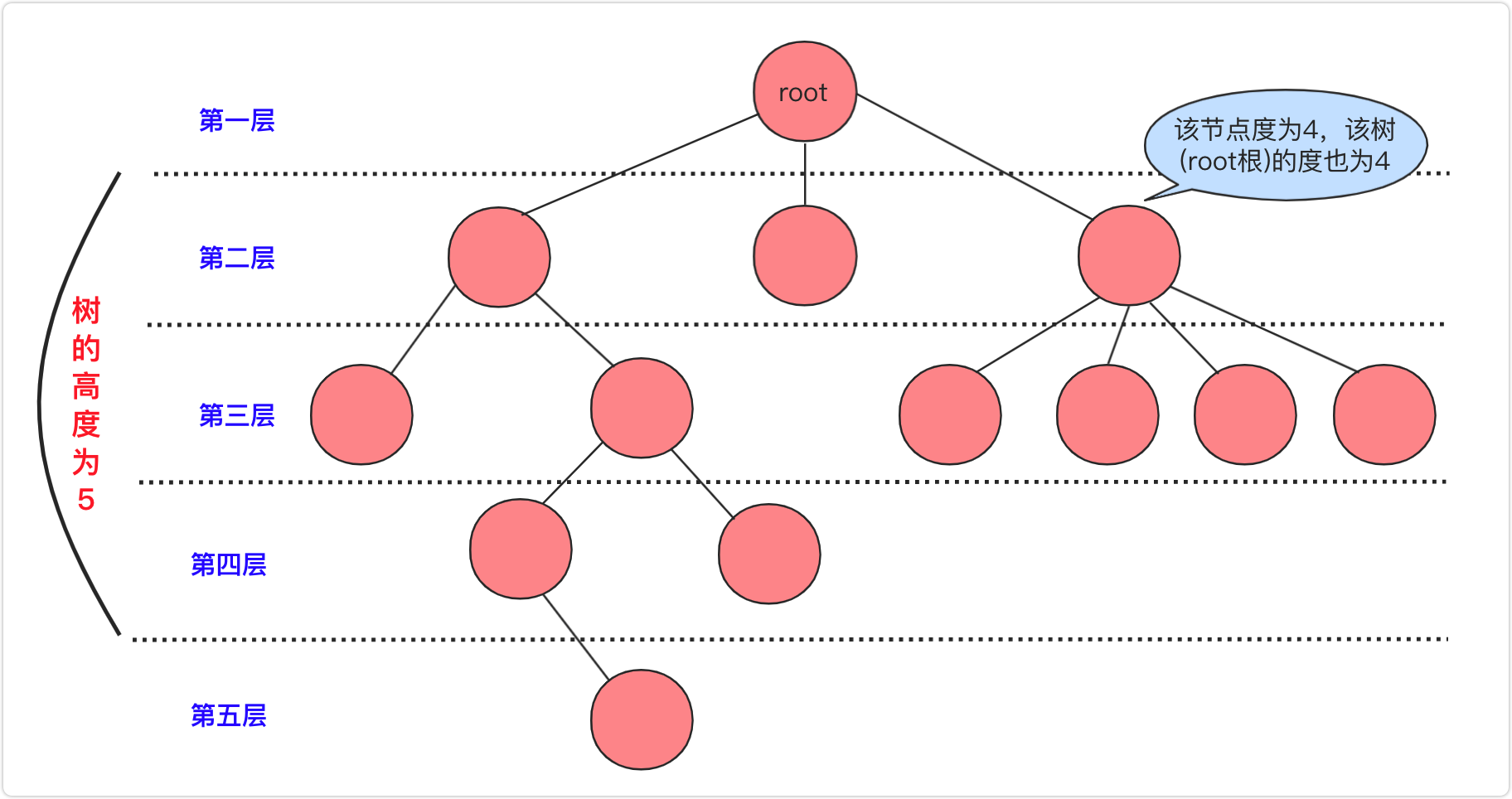

树是递归的，将树的任何一个节点以及节点下的节点都能组合成一个新的树，所以树的很多问题都是使用递归去完成。

根节点： 最上面的那个节点(root)，根节点没有父节点，只有子节点（0个或多个都可以）

层数： 一般认为根节点是第1层(有的也说第0层)，而树的高度就是层数最高(上图层数开始为1)节点的层数

节点关系:

• 父节点：连接该节点的上一层节点,
• 孩子节点: 和父节点对应，上下关系。而祖先节点是父节点的父节点(或者祖先）节点。
• 兄弟节点：拥有同一个父节点的节点们！

节点的度: 就是节点拥有孩子节点的个数(是直接连接的孩子不是子孙).

树的度: 就是所有节点中最大 (节点的度)。同时，如果度大于0的节点是分支节点,度等于0的节点是叶子节点（没有子孙）。

相关性质：

二叉树

二叉树是一树的一种，但应用比较多，所以需要深入学习，二叉树的每个节点最多只有两个子节点(但不一定非得要有两个节点)。

二叉树与度为2的树的区别：
1、度为2的的树必须有三个节点以上(否则就不叫度为二了，一定要先存在)，二叉树可以为空。
2、二叉树的度不一定为2,比如斜树。
3、二叉树有左右节点区分，而度为2的树没有左右节点的区分。

几种特殊二叉树：

满二叉树：高度为n的满二叉树有(2^n) -1个节点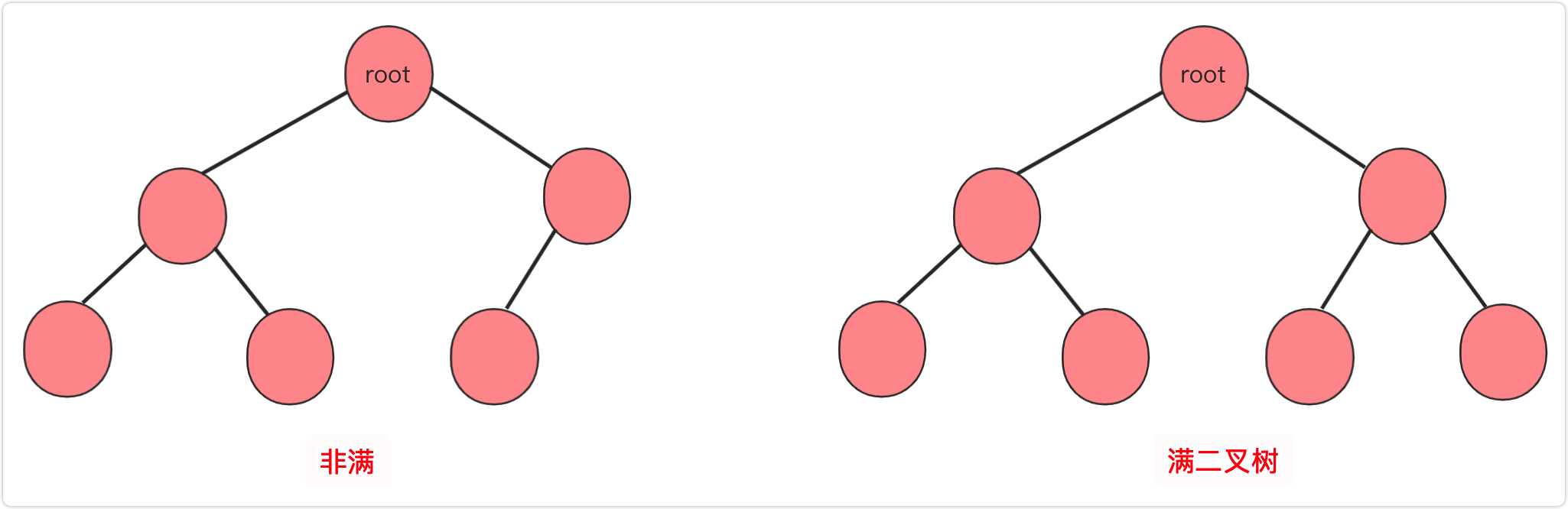

完全二叉树：上面一层全部满，最下一层从左到右顺序排列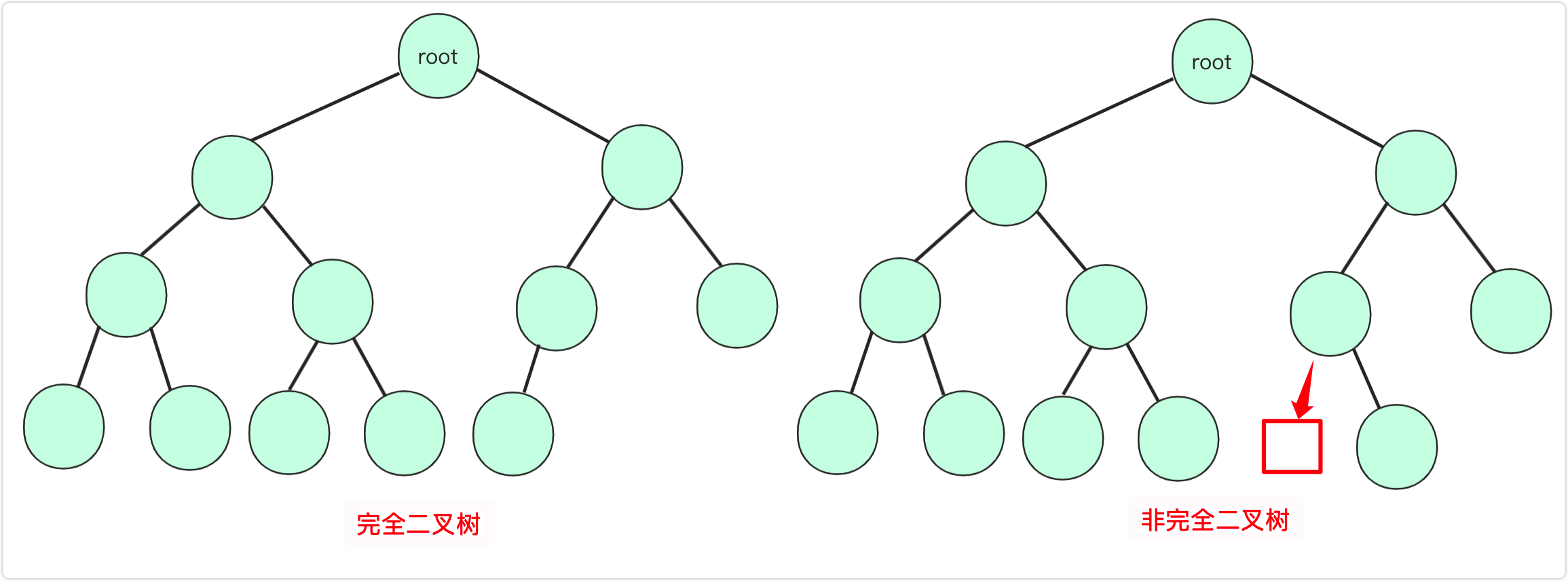

二叉排序树：树按照一定规则插入排序(本文详解)。
平衡二叉树：树上任意节点左子树和右子树深度差距不超过1(后文详解).

二叉树性质：

1、二叉树有用树的性质

2、非空二叉树叶子节点数=度为2的节点数+1.本来一个节点如果度为1.那么一直延续就一个叶子，但如果出现一个度为2除了延续原来的一个节点，会多出一个节点需要维系。所以到最后会多出一个叶子。

3、非空第i层最多有2^(i-1)个节点。

4、高为h的树最多有(2^h)-1个节点(等比求和)。

二叉树一般用链式存储，这样内存利用更高，但二叉树也可以用数组存储的(经常会遇到)，各个节点对应的下标是可以计算出来的，就拿一个完全二叉树若从左往右，从上到下编号如图：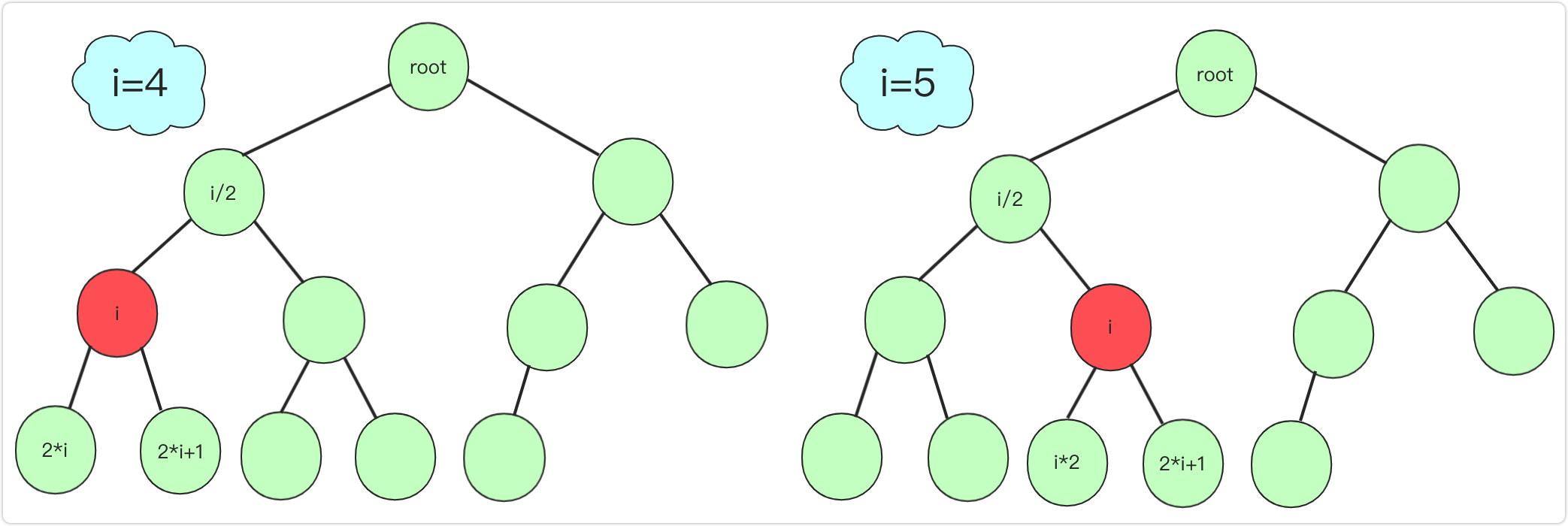

二叉排序(搜索)树

概念

前面铺垫那么多，咱们言归正传，详细讲解并实现一个二叉排序树，二叉搜索树拥有二叉树的性质，同时有一些自己的规则：

首先要了解二叉排序树的规则：从任意节点开始，节点左侧节点值总比节点右侧值要小。

例如一个二叉排序树依次插入15，6，23，7，4，71，5，50会形成下图顺序

构造

二叉排序树是由若干节点(node)构成的，对于node需要这些属性：left，right，和value。其中left和right是左右指针指向左右孩子子树，而value是储存的数据，这里用int 类型。

node类构造为：

class node {//结点
    public int value;
    public node left;
    public node right;
    public node()
    {
    }
    public node(int value)
    {
        this.value=value;
        this.left=null;
        this.right=null;
    }
    public node(int value,node l,node r)
    {
        this.value=value;
        this.left=l;
        this.right=r;
    }            
}

既然节点构造好了，那么就需要节点等其他信息构造成树，有了链表构造经验，很容易得知一棵树最主要的还是root根节点。
所以树的构造为：

public class BinarySortTree {
    node root;//根
    public BinarySortTree()
    {root=null;}
    public void makeEmpty()//变空
    {root=null;}
    public boolean isEmpty()//查看是否为空
    {return root==null;}
    //各种方法
}

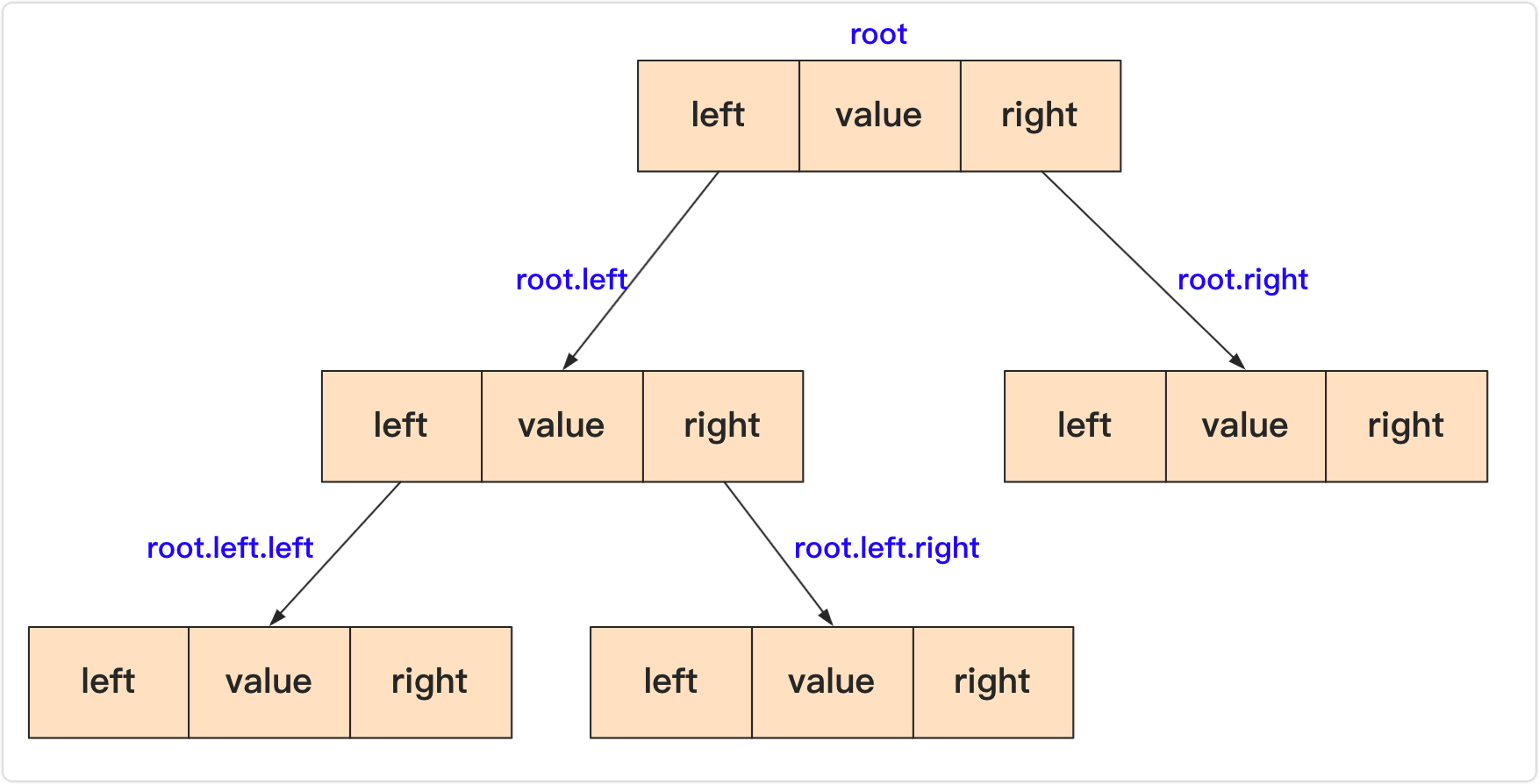
主要方法

既然已经构造好一棵树，那么就需要实现主要的方法,因为二叉排序树中每个节点都能看作一棵树。所以我们创建方法的是时候加上节点参数(方便一些递归调用)

findmax(),findmin()

findmin()找到最小节点：

因为所有节点的最小都是往左插入，所以只需要找到最左侧的返回即可，具体实现可使用递归也可非递归while循环。

findmax()找到最大节点：

因为所有节点大的都是往右面插入，所以只需要找到最右侧的返回即可，实现方法与findmin()方法一致。

代码使用递归函数

public node findmin(node t)//查找最小返回值是node，调用查看结果时需要.value
{
    if(t==null) {return null;}
    else if(t.left==null) {return t;}
    else return(findmin(t.left));    
}
public node findmax(node t)//查找最大
{
    if(t==null) {return null;}
    else if(t.right==null) {return t;}
    else return(findmax(t.right));    
}

isContains(int x)

这里的意思是查找二叉查找树中是否存在值为x的节点。

在具体实现上，根据二叉排序树左侧更小，右侧更大的性质进行往下查找，如果找到值为x的节点则返回true，如果找不到就返回false，当然实现上可以采用递归或者非递归，我这里使用非递归的方式。

public boolean isContains(int x)//是否存在
{
    node current=root;
    if(root==null) {return false;}
    while(current.value!=x&&current!=null) 
    {
        if(x<current.value) {current=current.left;}
        if(x>current.value) {current=current.right;}
        if(current==null) {return false;}//在里面判断如果超直接返回
    }
    //如果在这个位置判断是否为空会导致current.value不存在报错
     if(current.value==x) {return true;}        
    return false;        
}

insert(int x)

插入的思想和前面isContains(int x)类似，找到自己的位置(空位置)插入。

但是具体实现上有需要注意的地方，我们要到待插入位置上一层节点，你可能会疑问为什么不直接找到最后一个空，然后将current赋值过去current=new node(x)，这样的化current就相当于指向一个new node(x)节点，和原来树就脱离关系(原树相当于没有任何操作)，所以要提前通过父节点判定是否为空找到位置，找到合适位置通过父节点的left或者right节点指向新创建的节点才能完成插入的操作。

public node insert(int x)// 插入 t是root的引用
{
    node current = root;
    if (root == null) {
        root = new n