题目描述

给定我们一个长度为$nn$的数组，我们要找到一个和是最大的连续子数组，然后子数组有这么几个要求

1. 子数组是连续的
2. 如果有多个最长的，只留下来最长的那个
3. 最小的子数组长度为1，不存在0的情况
4. 返回数组空间不计入

题解

解法一：最简单的DP

实现思路

其实我比较推荐做这个题目之前去做一下剑指OFFER的第42题，因为这两个题目可以说就是多了一个最后的统计答案，而我们统计答案完全就是记录最后的一个位置即可，因为他们是连续的

假设我们的$arrayarray$数组长度是$nn$, 下标从0到n - 1

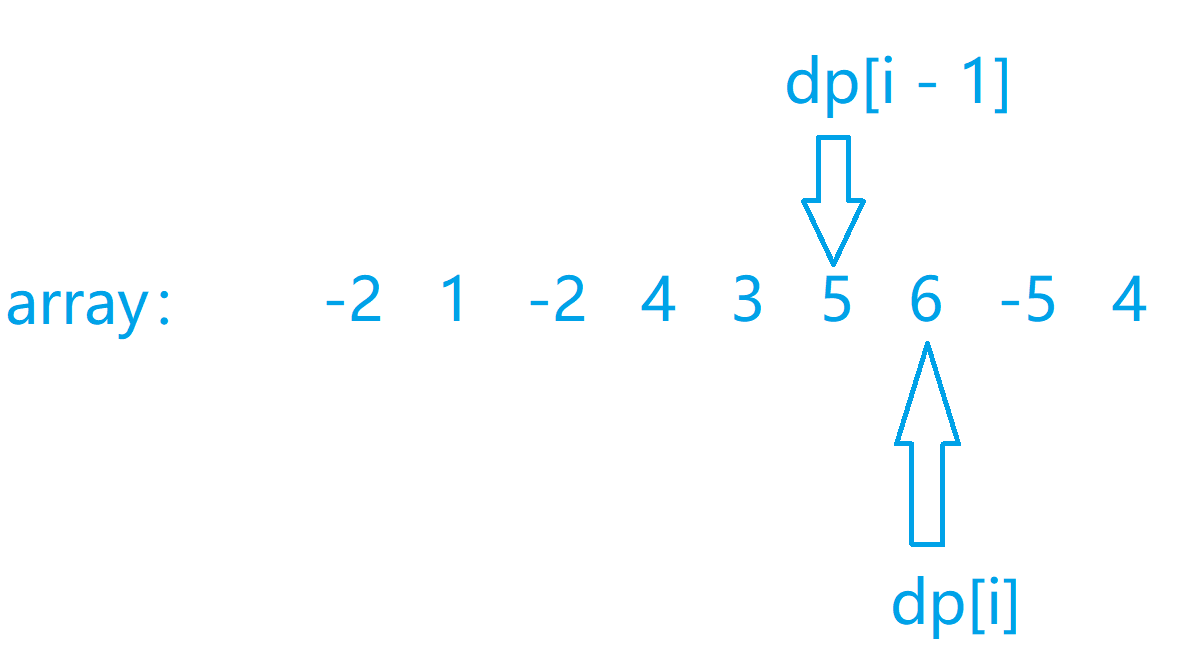
我们用dp[i]表示以第i个结尾的连续数组的最大和, 然后我们可以知道我们每一次的更新取决于$array[i]array[i]$和$dp[i-1]+array[i]dp[i\; -\; 1]\; +\; array[i]$的大小, 所以我们会有如下的状态转移方程

$dp[i]=max(dp[i-1]+array[i],array[i])dp[i]\; =\; max(dp[i\; -\; 1]\; +\; array[i],\; array[i])$

然后我们每次记录最大值的最后一个位置, 最后我们反向遍历一次就可以了

图解代码

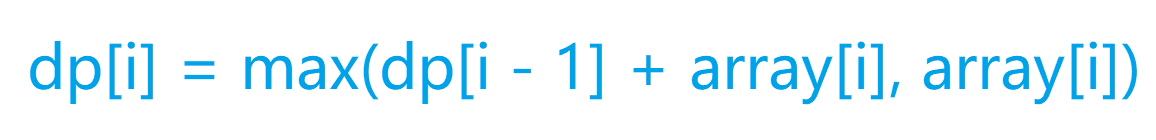
代码实现

class Solution {
   public:
    vector<int> FindGreatestSumOfSubArray(vector<int>& array) {
        vector<int> dp(array.size(), 0);
        dp[0] = array[0];
        // 我们一开始的第一个点就是我们原数组的第一个点
        int maxx = dp[0], pos = 0;
        // 这个是我们当前的最大值和我们结束的位置
        for (int i = 1; i < array.size(); i++) {
            dp[i] = max(dp[i - 1] + array[i], array[i]);
            // 状态转移方程
            if (dp[i] >= maxx) {
                pos = i, maxx = dp[i];
                // 如果我们当前的值比我们的最大值大了, 我们更新
            }
        }
        int res = 0;
        for (int i = pos; i >= 0; i--) {
            maxx -= array[i];
            if (maxx == 0) {
                res = i;
                // 这里不能直接返回, 因为我们可能前面会有更长的
            }
        }
        return vector<int>(array.begin() + res, array.begin() + 1 + pos);
    }
};

时空复杂度分析

时间复杂度: $O(n)O(n)$

理由如下: 我们简单的遍历了一次数组, 所以我们的时间复杂度是$O(n)O(n)$的

空间复杂度: $O(n)O(n)$

理由如下: 我们开辟了一个大小为$nn$的dp数组

解法二: 类似于双指针

实现思路

我们可以发现我们在解法一中, 其实我们每一次都是只用到了他的前一个状态, 也就是说并不是所有的状态都是有用的, 那么我们知道了这一点之后, 我们很容易的把空间压缩下来, 采用滚动数组的思想, 但是问题是我们如何保留最长的子数组, 这里我们就是可以想到我们上面的做法, 我们可以时刻维护着一个起始位置和终止位置, 然后一个最大值的起始位置和终点位置

代码实现

#include <bits/stdc++.h>
using namespace std;

class Solution {
   public:
    vector<int> FindGreatestSumOfSubArray(vector<int>& array) {
        int maxx = array[0], tmp = array[0];
        int l = 0, r = 1, resL = 0, resR = 0;
        // maxx是我们最大的值, tmp是每一次过程中的值
        // l和r是我们每次的子数组是左右边界, resLR是最后的答案
        while (r < array.size()) {
            tmp < 0 ? tmp = array[r], l = r : tmp += array[r];
            // 如果tmp<0，
            // 无论当前数是正还是负，但是sum已经是负数了，当前值加上sum肯定比当前值还要小，所以将sum更新为当前值
            if (tmp > maxx || tmp == maxx && (r - l) > (resR - resL)) {
                resL = l, resR = r;
            }
            maxx = max(maxx, tmp);
            r++;
        }
        return vector<int>(array.begin() + resL, array.begin() + 1 + resR);
    }
};

时空复杂度分析

时间复杂度: $O(n)O(n)$

理由如下: 我们简单的遍历了一次数组, 所以我们的时间复杂度是$O(n)O(n)$的

空间复杂度: $O(1)O(1)$

理由如下: 常量级别的空间