描述

题目描述

其实这个题目是一个很经典的题目, 就是我们有$NN$层楼, 我们有$KK$个物品, 然后我们要计算求解的就是我们在最坏的情况下得到的最小操作数

这个我们第一个最简单的想法可能就是一个个的比较去排除, 我们从第一层楼开始我们就是一直向上摔, 看看可不可以摔碎, 如果碎了, 那么正好就是这么一层楼, 如果没碎我们继续比较

但是这样的话我们就很原始很暴力很慢, 这时候凭借着大家做题的习惯肯定是要去进行一个二分, 我们每次取一半来测试, 如果鸡蛋的数量是无限的, 这样当然很好, 但是我们的鸡蛋的数量是有限个的, 那么我们肯定会第一个想法就是, 那我们$N-1N\; -\; 1$个鸡蛋二分, 最后剩下的鸡蛋我们一个个找呗

但是这样是不对的, 我举一个最经典的反例

假设我们现在有$100100$楼层, $22$个鸡蛋, 然后我们二分放在$5050$的地方扔, 我们发现碎了, 那么我们就只能是从$11$层开始一层层尝试着扔, 这样会很慢

有同学可能疑问为什么要从下向上, 因为我们鸡蛋碎了的话就没有办法使用了, 我们只能从最下面开始判断

那我们换位想一下, $100100$的算数平方根是$1010$, 我们是不是可以考虑一下十分, 我们十层一扔, 十层一扔, 这样就把我们的最小次数可以确定下来了

题解

解法一: 简单的记忆化DFS（会超时）

实现思路

首先我们假设我们在第$ii$层楼扔了鸡蛋之后, 我们存在两个情况就是

1. 鸡蛋碎了

那么我们的鸡蛋个数要减少一个, 楼层搜索的区间就从$[1,n][1,\; n]$变成了$[1,i-1][1,\; i\; -\; 1]$了

2. 鸡蛋没碎

那么我们鸡蛋的个数不变, 但是楼层从$[1,n][1,\; n]$变成了$[i+1,n][i\; +\; 1,\; n]$

然后这个是对于我们每一层的两种情况，我们每次为了找到最坏的一个情况，我们要在所有的楼层中选择一个最坏的情况，所以我们每次$dfsdfs$的时候，我们还要进行操作的就是在所有楼层中找到最坏的一个情况，然后我们如何判断当前楼的最坏情况呢？事实上，当前的这层楼就会出现我们上述的两个情况，鸡蛋碎了和鸡蛋没碎，根据这两种情况，分别进入下一重$dfsdfs$，然后我们为了减少重复计算，我们可以把我们目前已经算过的鸡蛋和楼层数记录下来，然后我们的递归终止条件就很明显了，第一个就是当我们只有一个鸡蛋的时候，和当我们没有楼层或者这个这对鸡蛋数目和楼层数目我们曾经已经记录过了，我们可以直接返回值

那么我们的记忆化搜索的代码就可以出来了

class Solution {
    map<pair<int, int>, int> mp;
    
// pair里面第一个存的是楼层数，第二个存的是鸡蛋数
   public:
    int dfs(int n, int k) {
        if (k == 1) return n;
        if (n == 0) return 0;
//         这个是只有一个鸡蛋和没有楼层
        if (mp[{n, k}]) return mp[{n, k}];
//         如果这个之前出现过
        int res = INT_MAX;
        for (int i = 1; i <= n; i++)
            res = min(res, max(dfs(n - i, k), dfs(i - 1, k - 1)) + 1);
//         因为我们要求取的是最坏的情况，所以我们要去一个最大值
        mp[{n, k}] = res;
//         记录一下
        return res;
    }
    int solve(int n, int k) { return dfs(n, k); }
};

时空复杂度分析:

时间复杂度: $O(k\ast n^2\ast log(nk))O(k\; *\; n\; ^\; 2\; *\; log(nk))$

理由如下: 我们记忆化的话事实上我们是把所有的情况都会遍历到, 那么我们所有的情况是什么呢? 就是我们$k\ast nk\; *\; n$, 但是这里不是简单的$k\ast nk\; *\; n$, 我们还要考虑到这样的一个事情, 我们每次$dfsdfs$会进行一个循环, 那么我们的时间复杂度又要再乘上一个$nn$, 这里还没结束, 我们因为用了一个$mapmap$取存储我们的所有情况, 则我们会带上一个$loglog$的复杂度

空间复杂度: $O(k\ast n)O(k\; *\; n)$

理由如下: 存储了所有的可能情况

解法二: 重新定义状态方程

实现思路

我们第一种做法事实上就是一个穷举的思想, 我们得考虑如何优化这个问题, 那么我们反向思考这个问题, 我们让第一维还是有多少个鸡蛋, 然后让我们的第二维变成最多允许扔鸡蛋的次数, 这样我们可以知道最高的楼层数

比如我们有一个鸡蛋, 我们最多可以扔七次, 那么我们是不是很容易的就可以知道了我们确定了楼层七可以使得鸡蛋恰好摔不碎

然后我们可以发现有这么两个特点

1. 无论在那一层楼扔鸡蛋, 鸡蛋只可能是没有碎或者碎了, 碎了就是楼下, 没碎就是楼上

2. 无论上下楼, 总的楼层数 = 楼上层数 + 楼下层数 + 1

然后我们思考我们的$DPDP$数组的含义是什么？

比如我们有一个$dp[k][m]==ndp[k][m]\; ==\; n$，这个代表的就是我们当前有$kk$个鸡蛋, 我们最多可以扔$mm$次, 这样我们最坏的情况下我们可以测试一栋层数为$nn$的楼

那么我们拿一个例子来解释一下:

假设我们$dp[1][5]==5dp[1][5]\; ==\; 5$, 这个是不是就是很好理解了,我们只有一个鸡蛋, 我们最多可以扔$55$次, 那么我们可以知道的这个楼的最高的高度是不是就是$55$

那我们状态转移方程根据我们上面的含义和两个特点, 我们是不是可以画这样一个图

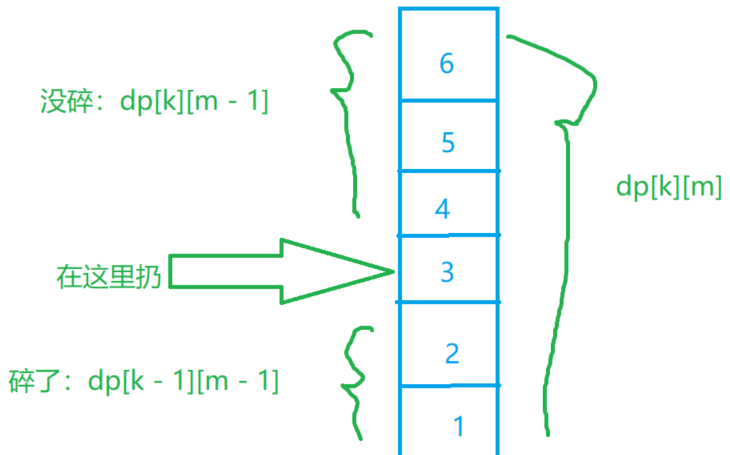
我们当前的总楼层数就是我们楼上的楼层数加上我们楼下楼层数加上我们当前这层

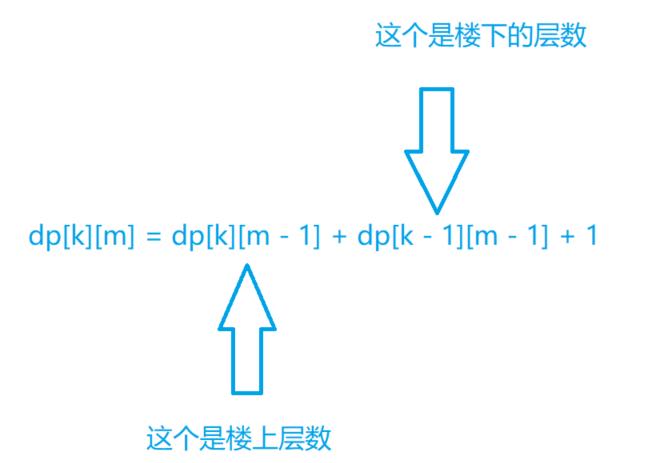
那么我们就可以得到这样的一个状态方程

$dp[k][m]=dp[k][m-1]+dp[k-1][m-1]+1dp[k][m]\; =\; dp[k][m\; -\; 1]\; +\; dp[k\; -\; 1][m\; -\; 1]\; +\; 1$

代码实现

class Solution {
   public:
    int solve(int n, int k) {
        vector<vector<int>> dp(k + 1, vector<int>(n + 1, 0));
        int m = 0;
        while (dp[k][m] < n) {
            m++;
            for (int i = 1; i <= k; i++)
                dp[i][m] = dp[i][m - 1] + dp[i - 1][m - 1] + 1;
        }
//         满足条件的方程
        return m;
    }
};

时空复杂度分析:

时间复杂度: $O(k\ast m)O(k\; *\; m)$

理由如下: $kk$是我们的鸡蛋数量, $mm$是我们最后的楼层数, 因为我们满足条件就跳出来了

空间复杂度: $O(k\ast n)O(k\; *\; n)$

理由如下: 存储了所有的可能情况

代码实现

我们发现我们刚才的代码会炸内存, 那么我们怎么办呢?

我们可以用递归来写

class Solution {
   public:
    int dfs(int k, int m) {
        if (m == 1 or k == 1) return m + 1;
        return dfs(k - 1, m - 1) + dfs(k, m - 1);
        // 这个就是把状态转移方程变成递归形式
    }

    int solve(int n, int k) {
        int m = 1;
        while (dfs(k, m) <= n) m++;
        // 寻找$m$次
        return m;
    }
};

时空复杂度分析:

时间复杂度: $O(k\ast m)O(k\; *\; m)$

理由如下: $kk$是我们的鸡蛋数量, $mm$是我们最后的楼层数, 因为我们满足条件就跳出来了

空间复杂度: $O(m)O(m)$

理由如下: 系统的递归栈

动态规划和搜索的关系

其实我们有时候会发现, 某些动态规划的问题其实可以转换为搜索来写, 其实他们俩个一个是自底而上, 一个是自顶而下