前缀/中缀/后缀----表达式之间的相互转换
三种表达式
- 前缀表达式: +ab, 这种也叫做波兰式
- 中缀表达式: a+b, 这种正常表达式需要带括号, 而波兰式不用带括号
- 后缀表达式: ab+, 这种也叫做逆波兰式
三者之间互相转换
中缀->前缀 and 中缀->后缀
a+b <----> (a)+(b)
将括号部分的(a)和(b)视作子表达式
随后将二目运算符移到前面
得到+(a)(b), 也即+ab, 这就是前缀(波兰)表达式
将二目运算符移到后面
得到(a)(b)+, 也即+ab, 这就是后缀(逆波兰)表达式
转换方法:
将中缀表达式(a+b)*c+d-(e+g)*h转换为前缀表达式
法 1: 加括号法/直接法
注意每一个配对的括号内都包含两个子表达式和一个运算符
((((a+b)*c)+d)-((e+g)*h))
随后将同一括号内的运算符提取到括号前
-(+(*(+(ab)c)d)*(+(eg)h))
随后将括号去除得到:-+*+abcd*+egh即为前缀表达式
变体:
将该中缀表达式转换为后缀表达式
使用加括号法得到((((ab)+c)*d)+((eg)+h)*)-
去掉括号从而得到ab+c*d+eg+h*-法 2: 遍历树法
将中缀表达式(a+b)*c+d-(e+g)*h写作表达式树
对其进行先前序遍历得到前缀表达式
-+*+abcd*+egh
变体:
对其进行后序遍历得到后缀表达式法 3: 入栈法
中缀转后缀规则如下:
从左到右扫描中缀表达式
遇到操作数直接将其写出
遇到操作符则将其入栈, 首先令其与栈顶运算符比较
若优先级小于等于, 则栈顶出栈
一直循环, 直到该运算符大于栈顶优先级才入栈
栈底直接入栈, 栈顶全部出栈
左括号相当于部分栈底, 右括号相当于部分栈顶, 均直接入栈出栈
变体:
中缀转前缀则是从右向左, 注意小于栈顶优先级即出栈, 所得结果逆序
对比注意点:
中缀转后缀常用, 从左到右, 小于等于即出栈(遇到+-则+-也出栈)
中缀转前缀相反, 从右到左, 小于才出栈(遇到+-,本身不出栈)(容易扎堆在前面出栈)
后缀->中缀 and 前缀->中缀
就是上面过程的逆过程
转换方法
将ab+c*d+eg+h*-转换为中缀表达式
法 1: 从左到右逐个比较
遇到连续两个表达式加一个运算符的组合
即将其转换为中缀, 运算流程如下:
(a+b)c*d+eg+h*-
((a+b)*c)d+eg+h*-
(((a+b)*c)+d)eg+h*-
(((a+b)*c)+d)(e+g)h*-
(((a+b)*c)+d)((e+g)*h)-
((((a+b)*c)+d)-((e+g)*h))
(a+b)*c+d-(e+g)*h法 2:
使用后缀表达式扫描推栈法

变体:
将-+*+abcd*+egh转换为中缀表达式
法 1: 与上面大同小异
法 2: 将栈从右到左压入, 同样是遇到运算符即建单点树
后缀->前缀 and 前缀->后缀
法 1: 与上述过程相似, 先用括号标注
随后将后缀的运算符移到前面(反之亦然)
法 2: 将后缀变为表达式树
随后将表达式树转换为前缀表达式(反之亦然)
法 3: 使用栈计算
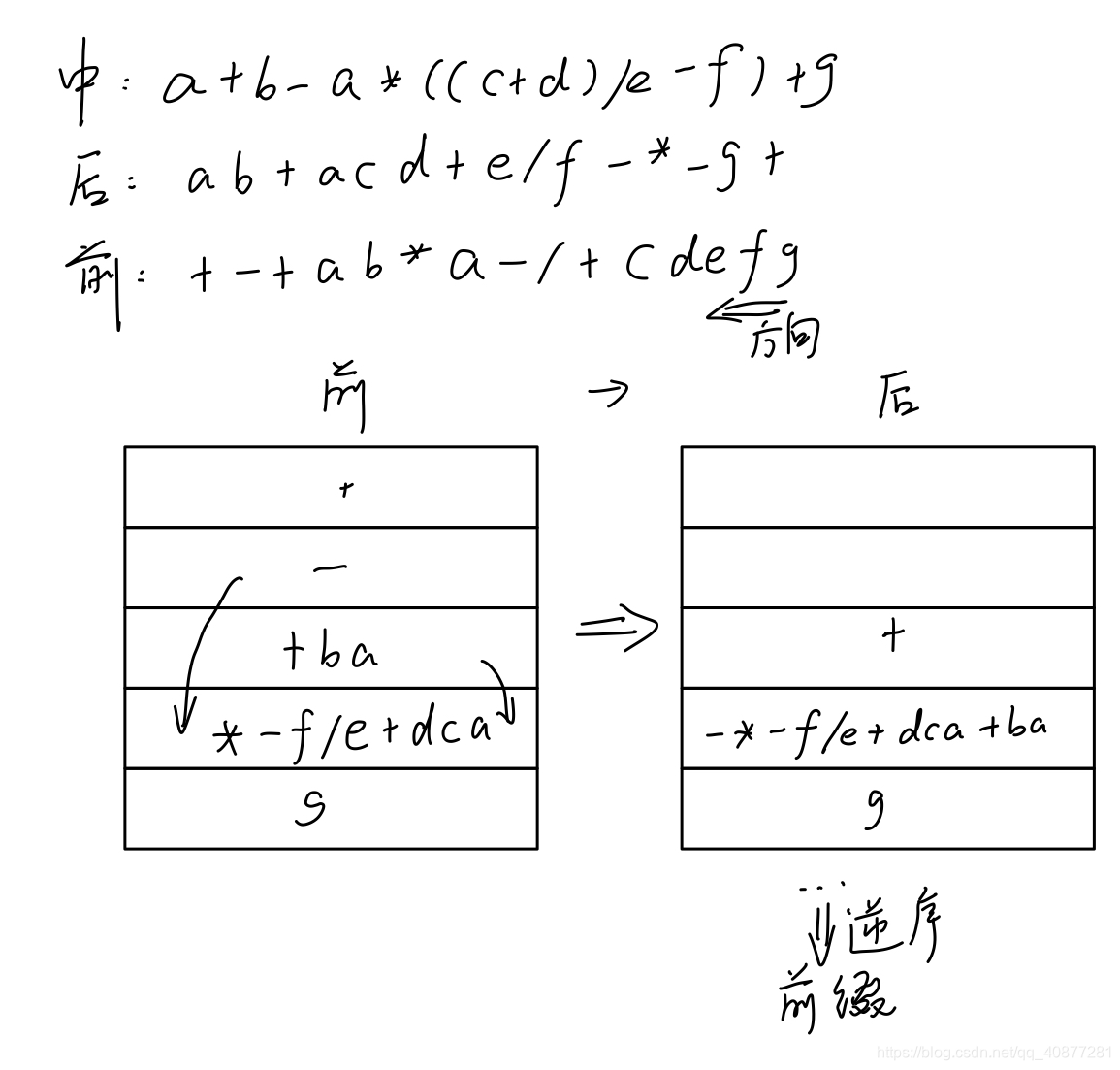
后缀转前缀, 从前到后扫描, 遇到一运算符两子表达式形式则符号前移, 中间表达式后移, 如图所示:
> 前缀转后缀, 从后到前扫描, 遇到一运算符两子表达式形式同样符号前移, 中间子表达式后移, 最后结果逆序, 如图所示:
代码实现
中缀转后缀
#include <iostream>
using namespace std;
const int maxSize = 20;
int getPriority(char i)
//得到符号的优先级
{
switch (i)
{
case '+':
case '-':
return 1;
case '*':
case '/':
return 2;
}
}
int infixToPostfix(char infix[],
char s2[])
{
char s1[maxSize];
//符号堆栈
int top1 = -1, top2 = -1;
//top1是符号堆栈的标号, top2是结果数组的标号
int stackMax = 0;
//记录堆栈最大处的标号
int i = 0;
//指向原数组的标号
while (infix[i] != '\0')
//控制循环的原数组循环的末尾
{
if (('a' <= infix[i] &&
infix[i] <= 'z') ||
(('0' <= infix[i] &&
infix[i] <= '9')))
//如果选到数字或者字母, 直接写入结果数组
{
s2[++top2] = infix[i];
i++;
}
else if (infix[i] == '(')
//如果遇到左括号, 直接写入符号堆栈
{
s1[++top1] = '(';
if (top1 > stackMax)
stackMax = top1;
i++;
}
else if (infix[i] == '+' ||
infix[i] == '-' ||
infix[i] == '*' ||
infix[i] == '/')
//如果遇到运算符则分类讨论
{
if (top1 == -1 ||
s1[top1] == '(' ||
getPriority(infix[i]) >
getPriority(s1[top1]))
//若在栈底, 在括号底, 或者操作符优先级高, 则操作符入栈
{
s1[++top1] = infix[i];
if (top1 > stackMax)
stackMax = top1;
i++;
}
else //否则出栈
s2[++top2] = s1[top1--];
}
else if (infix[i] == ')')
//如果遇到右括号, 则将其与对应左括号之间的符号出栈
{
while (s1[top1] != '(')
s2[++top2] = s1[top1--];
top1--;
i++;
}
}
while (top1 != -1)
//这里将堆栈中剩余的符号推出堆栈
s2[++top2] = s1[top1--];
return stackMax + 1;
//这里top1是堆栈标号, 必须+1才是数目
}
int main()
{
int top2 = -1;
char s2[maxSize];
char infix[maxSize] = "a+b-a*((c+d)/e-f)+g";
cout << infixToPostfix(infix, s2) << endl;
int i = 0;
while (s2[i] != '\0')
cout << s2[i++];
cout << endl;
return 0;
}
/*结果
5
ab+acd+e/f-*-g+
*/
中缀转前缀
#include <iostream>
using namespace std;
const int maxSize = 20;
int getPriority(char i)
//得到符号的优先级
{
switch (i)
{
case '+':
case '-':
return 1;
case '*':
case '/':
return 2;
}
}
int getStringSize(char s[])
//注意仅用于字符数组
{
int i = 0;
while (s[i] != '\0')
i++;
return i;
}
int infixToPrefix(char infix[],
char s2[])
{
char s1[maxSize];
//符号堆栈
int top1 = -1, top2 = -1;
//top1是符号堆栈的标号, top2是结果数组的标号
int stackMax = 0;
//记录堆栈最大处的标号
int i = getStringSize(infix) - 1;
//指向原数组的标号, 注意转前缀是逆序
while (i != -1)
//控制循环的原数组循环的结束
{
if (('a' <= infix[i] &&
infix[i] <= 'z') ||
(('0' <= infix[i] &&
infix[i] <= '9')))
//如果选到数字或者字母, 直接写入结果数组
{
s2[++top2] = infix[i];
i--;
}
else if (infix[i] == ')')
//如果遇到右括号, 直接写入符号堆栈
{
s1[++top1] = ')';
if (top1 > stackMax)
stackMax = top1;
i--;
}
else if (infix[i] == '+' ||
infix[i] == '-' ||
infix[i] == '*' ||
infix[i] == '/')
//如果遇到运算符则分类讨论
{
if (top1 == -1 ||
s1[top1] == ')' ||
getPriority(infix[i]) >=
getPriority(s1[top1]))
//若在栈底, 在括号底, 或者操作符优先级高或者相等, 则操作符入栈
//注意转前缀时候入栈更简单, 优先级相同即可入栈
{
s1[++top1] = infix[i];
if (top1 > stackMax)
stackMax = top1;
i--;
}
else //否则出栈
s2[++top2] = s1[top1--];
}
else if (infix[i] == '(')
//如果遇到左括号, 则将其与对应右括号之间的符号出栈
{
while (s1[top1] != ')')
s2[++top2] = s1[top1--];
top1--;
i--;
}
}
while (top1 != -1)
//这里将堆栈中剩余的符号推出堆栈
s2[++top2] = s1[top1--];
return stackMax + 1;
//这里top1是堆栈标号, 必须+1才是数目
}
int main()
{
int top2 = -1;
char s2[maxSize];
char infix[maxSize] = "a+b-a*((c+d)/e-f)+g";
cout << infixToPrefix(infix, s2) << endl;
int i = getStringSize(s2) - 1;
while (i != -1)
cout << s2[i--];
cout << endl;
return 0;
}
/*结果
6
+-+ab*a-/+cdefg
*/
参考:https://blog.csdn.net/qq_36631580/article/details/88685588 参考:https://www.cnblogs.com/chensongxian/p/7059802.html
数据结构大篇幅笔记记录




 Momenta公司福利 280人发布
Momenta公司福利 280人发布