题解 | #跳跃游戏(三)#
跳跃游戏(三)
http://www.nowcoder.com/practice/14abdfaf0ec4419cbc722decc709938b
描述
题目描述
给我们一个数组,然后我们的起始位置是,然后我们数组里面的每一个元素就是我们每次可以跳的最大的一个距离,问最少几次可以跳到终点
注意: 如果跳不到最后的话,我们输出,如果我们数组长度为,返回
样例解释
样例输入:
[2,1,3,3,0,0,100]
我们从第一个地方开始跳,我们发现可以从
注意: 我们这里跳的最长的长度是我们的这个数组的值,事实上我们其实可以不跳这么远,跳近一点
所以我们最后的样例输出就是
3
题解
解法一 : 贪心
解题思路
首先我们可以想这么一个问题,我们一定是从第号点开始跳跃,那么我们可以跳到从这里面所有点中的一个点,那么我们的指针就遍历这些点去寻找我们这些点可以到达的最远的点是什么,然后当我们已经扫到了我们的的这个位置的时候,我们就可以更新一下我们找到的最远点,在更新最远点的时候把步数增加,这时候我们有一个要注意的就是,我们最后一个点不需要判断,因为我们在之前如果可以到达最后的话,我们一定最后可以到达的最远点是大于等于我们最后一个位置的,所以我们不需要判断最远点
贪心的简单证明
首先因为我们每一次的步骤我们都是把我们可能到达的点遍历了一次,寻找下一次可以到达的最大的点,然后我们可以用反证法,如果我们存在一个点到下一个点内的区间可以到达的点更大,而我们却选择了另一个点,这时候是与我们每次寻找未来可以到达最大点,最大区间是冲突的,因为我们一定是选择了未来可以跳的最长的点,那么这个可以保证的是其他点可以跳的范围一定比这个点短,那么我们就是可以保证短的点可以到达的点,我们长的点一定也是可以到达的,所以我们每一次可以直接选择可以到达更远的一个点
图解代码
我们拿我们上面的样例[2,1,3,3,0,0,100]举例子
首先第一步
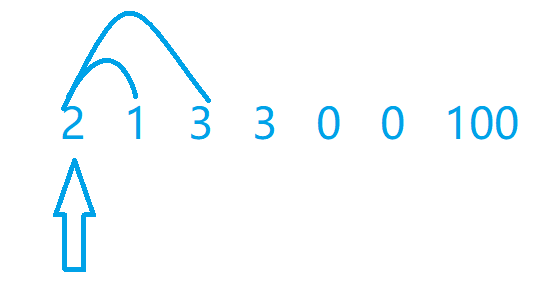
然后我们选择未来可以跳的更远的点
然后我们继续把指针移动到
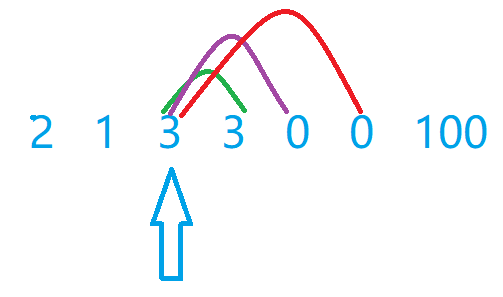
然后我们发现我们从开始,可以到达未来最远的点就是下一个然后我们移动指针
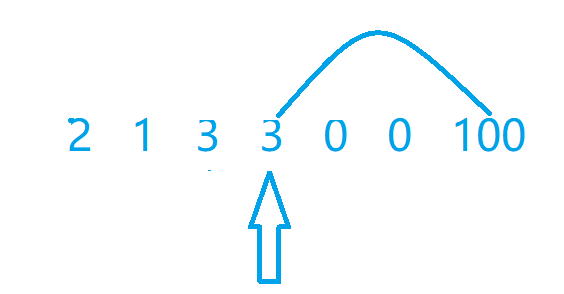
然后我们直接可以到达最后,直接结束,我们总的步数就是
代码实现
class Solution {
public:
int minJumpStep(vector<int>& nums) {
int len = nums.size();
// 获取数组长度
if (len == 0) return -1;
// 如果是 0 按照题意返回 -1
if (len == 1) return 0;
// 如果是 1 那么我们直接可以返回 0
int pos = nums[0], end = nums[0], step = 1;
// 我们把可以目前区间内可以到达的最远距离设置为我们第 0 个的可以跳的距离
// 然后我们第一次的边界也是我们第 0 个可以跳的最远距离
// 因为我们这时候数组至少有两个及以上的元素,我们可以直接算是跳了一步
for (int i = 1; i < len - 1; i++) {
// 我们从 1 开始遍历到我们最后一个元素前面的一个元素,这个在前面解析中有
if (pos >= i) {
// 如果我们的可以到达的最终位置大于等于当前位置我们继续
pos = max(pos, i + nums[i]);
// 每次获取最大值
if (end == i) end = pos, step++;
// 如果已经到达了我们的边界,我们更新我们的边界值,然后把我们的步数加 1
}
}
if (end < len - 1) return -1;
// 如果最后我们的边界值没有到达我们的最后一个元素的位置,我们返回 -1
return step;
}
};
时空复杂度
时间复杂度:
理由如下:因为我们只把整个数组遍历了一遍,所以我们的时间复杂度就是数组的长度,所以时间复杂度为
空间复杂度:
理由如下:因为我们只引用了常数级别的空间所以我们的空间复杂度是的
解法二:动态规划
解题思路
我们可以简单的想一下,我们第个点是怎么来的,是不是所有可以到达第个点的所需要的步骤即可
所以我们可以很容易得到以下的一个状态转移方程
当我们的时候我们上述的状态转移方程成立
代码实现
class Solution {
public:
int minJumpStep(vector<int>& nums) {
int len = nums.size();
// 获取字符串长度
if (len == 0) return -1;
if (len == 1) return 0;
// 这个依据题意,我们直接返回数值
vector<int> dp(len, INT_MAX / 2);
// 我们开辟do数组,然后初始化为最大值除2,避免出现溢出的麻烦
dp[0] = 0;
// 我们第一位不用移动,是我们的起始点
for (int i = 1; i < len; i++)
// 遍历我们整个数组
for (int j = 0; j < i; j++)
// 找到 i 之前所有可以到达 i 的点
if (nums[j] + j >= i) dp[i] = min(dp[i], dp[j] + 1);
// 得到最小的步数
return dp[len - 1] == INT_MAX / 2 ? -1 : dp[len - 1];
// 如果最后可以到达,返回步数,不可以到达,返回 - 1
}
};
时空复杂度
时间复杂度:
理由如下:为我们的数组长度,在我们求取状态转移方程的时候,我们可以发现,我们其实是把每一个点前面的点都遍历了一次,所以时间复杂度是的
空间复杂度:
理由如下:我们开辟了一个跟我们数组长度大小一样的数组,所以我们的空间复杂度就是的
贴一个图纪念一下

主要是机试题目的题目讲解和做法

 查看4道真题和解析
查看4道真题和解析

