神经网络简介

神经网络是当前一个十分火热的机器学习模型之一,通过神经网络,当代工业实现了许多惊人的进步,比如人脸检测的出现,人工智能语音的出现等等.

神经网络本质

神经网络看似十分的玄乎,但其实在知乎上曾有过一个问题,“如何看待神经网络的本质就是多层复合函数?”,那又为什么说神经网络的本质是多重复合函数呢?且听我细细道来.

神经网络结构分析

输入层

神经网络用于接受输入的第一层称作输入层,其维度与输入数据的特征维度相同.

隐藏层

隐藏层是介于输入层和输出层间的多层网络结构,通过加宽或加深隐藏层的层数,可以提高神经网络的拟合能力.但同时也会带来更大的资源消耗.

输出层

输出层是最后一层的层级结构,该层链接着最后的损失函数.其输出的维度一般同类别的数量相同.

激活函数

激活函数用于各层之间,用于增加各层的拟合能力.对于损失函数如果能正确选择较好的损失函数的话,可以很好的提高神经网络的性能.tanh激活函数图像如下:

relu损失函数图像如下:

sigmoid损失函数图像如下:

损失函数

损失函数是用于衡量整个模型的性能,最熟悉的就是MSE平方差损失函数:
$$MSE=\frac{1}{n}\sum _{i=0}^n(y_i-f(x_i){)}^2$$
同样还有交叉熵损失函数:
$$CrossEntropy=\frac{1}{n}\sum _{i=0}^n{y}_i\ast log(f(x_i))$$

神经网络公式推导

这里结合后面的代码实战内容,我们仅仅对一层的浅层神经网络进行推导和计算.

前向传播

因为只有一层,所以前向传播较为简单.
$$y_k^{\prime }=\frac{e^{w_k{x}_k}}{{\sum }_{i=0}^n{e}^{w_i{x}_i}}$$
同时计算对应的损失函数:
$$Loss=\sum _{i=0}^n{y}_k\ast log(y_k^{\prime })$$

梯度下降

梯度下降算法是神经网络的核心,也是其拟合能力极强的原因.其主要的原理是借助于梯度的局部变化最大来尽可能的拟合对应的损失函数的最小值.
将梯度下降用到我们的权重更新中就可以完成整个网络.
首先可以看到交叉熵函数仅仅对标签为1的类别进行计算值,因此可以计算如下:
$$Loss=log(y^{\prime })$$
计算$y^{\prime }$偏导如下:
$$\frac{\partial Loss}{\partial y^{\prime }}=\frac{1}{y^{\prime }}$$
但因为我们需要更新的是参数$w$,因此再对$w$求偏导.当k等于i的时候:
$$\begin{array}{rl}\frac{\partial y^{\prime }}{\partial z}& =\frac{\partial (\frac{e^{z_k}}{{\sum }_{i=1}^n{e}^{z_i}})}{\partial z}\\ & =\frac{e^{z_k}{\sum }_{i=1}^n{e}^{z_i}-(e^{z_k}{)}^2}{({\sum }_{i=1}^n{e}^{z_i}{)}^2}\\ & =y_k^{\prime }(1-y_k^{\prime })\end{array}$$
当i不等于k的时候:
$$\begin{array}{rl}\frac{\partial y^{\prime }}{\partial z}& =\frac{\partial (\frac{e^{z_k}}{{\sum }_{i=1}^n{e}^{z_i}})}{\partial z}\\ & =\frac{-e^{z_t}\ast e^{z_i}}{({\sum }_{i=1}^n{e}^{z_i}{)}^2}\\ & =y_t^{\prime }\ast y_i^{\prime }\end{array}$$
结合上面的求导得到,当i=k时:
$$\begin{array}{rl}\frac{\partial Loss}{\partial y^{\prime }}\frac{\partial y^{\prime }}{\partial z}& =(1-y_k^{\prime })\end{array}$$
当i!=k时:
$$\begin{array}{rl}\frac{\partial Loss}{\partial y^{\prime }}\frac{\partial y^{\prime }}{\partial z}& =y_k^{\prime }\end{array}$$
进一步的对$w$进行求导得到最后的导数,当i=k的时候,
$$\begin{array}{rl}\frac{\partial Loss}{\partial w}& =(1-y_k^{\prime })\ast w\end{array}$$
当i!=k时,有:
$$\begin{array}{rl}\frac{\partial Loss}{\partial w}& =y_k^{\prime }\ast w\end{array}$$
通过上面计算得到的公式,用于更新对应的权重$w$,设定学习率为$a$:
$$w_t=w_{t-1}+a\ast \frac{\partial Loss}{\partial w}$$

代码实战

这里采用的iris数据集进行的实验,全程不使用框架而是采用numpy数据库进行搭建,这里尽可能使用了交叉验证等方法来减小过拟合,但是由于数据确实比较少,

"""numpy实现简单神经网络"""
from collections import Counter

import numpy as np
import pandas as pd
from sklearn.model_selection import StratifiedKFold, train_test_split
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
import warnings

warnings.filterwarnings('ignore')


def Cross_entropy(x, y):
    # 交叉熵损失函数
    loss = -np.log(x) * y
    n = len(loss)
    return sum(np.sum(loss, axis=1) / n)  # 行求和


def softmax(x):
    x = np.exp(x)
    sumval = np.reshape(np.sum(x, axis=1), (x.shape[0], 1))
    return x / sumval


def sigmoid(x):
    # sigmoid激活函数
    return 1 / 1 + np.exp(-x)


def Derivative_sigmoid(x):
    # sigmoid函数的导数
    return np.matmul(sigmoid(x), (1 - sigmoid(x)).T)


def Accuracy(prediction, labels):
    prediction = np.argmax(prediction, axis=1)
    labels = np.argmax(labels, axis=1)
    counter = Counter(prediction + labels)
    return counter[2]/len(prediction)


if __name__ == '__main__':
    # 对读取的数据进行预处理.
    iris = pd.read_csv("iris.csv", index_col=0)
    data, labels = np.array(iris.iloc[:, :4]), iris.iloc[:, -1]

    # 将标签转化成对应的onehot编码。
    onehot_encoder = OneHotEncoder()

    # 将文字转换成对应的数字
    label_encoder = LabelEncoder()
    labels = label_encoder.fit_transform(labels)
    labels = np.reshape(labels, (-1, 1))
    labels = onehot_encoder.fit_transform(labels).toarray()

    # hidden_size为隐藏神经元数目，output_size为输出的类别数
    hidden_size, output_size = 100, labels.shape[1]

    # 根据输入得到对应的输入维度
    input_size = len(data[0])

    # 构建隐藏层权重，shape为(I，O)
    weight = np.random.random_sample((input_size, output_size))

    # 设置超参数轮次Epoch和Batch_size
    Epoch, Batch_Size, learning_rate = 1, 32, 0.01

    # 分割数据集，留下20%的数据来预测模型的结果.
    traindata, testdata, trainlabels, testlabels = train_test_split(data, labels, test_size=0.2)
    for e in range(Epoch):
        # 训练Epoch个轮次
        kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=2020)  # 五折交叉验证
        for train, valid in kfold.split(data, [0] * len(labels)):
            traindata, trainlabels, validdata, validlabels = data[train], labels[train], data[valid], labels[valid]
            loss = 0
            for b in range(0, len(traindata), Batch_Size):
                batch_data, batch_labels = traindata[b:b + Batch_Size], trainlabels[b:b + Batch_Size]

                # output_data维度应该为（B，H）*(H, O)=(B, O)
                output_data = softmax(np.matmul(batch_data, weight))

                # 计算对应的交叉熵损失函数
                loss += Cross_entropy(output_data, batch_labels)

                # Gradient Descent 梯度下降更新, 首先更新输出层的权重.
                output_layer_delta = (batch_labels - output_data).T
                output_w_delta = np.matmul(output_layer_delta, batch_data) / Batch_Size
                weight += learning_rate * output_w_delta.T
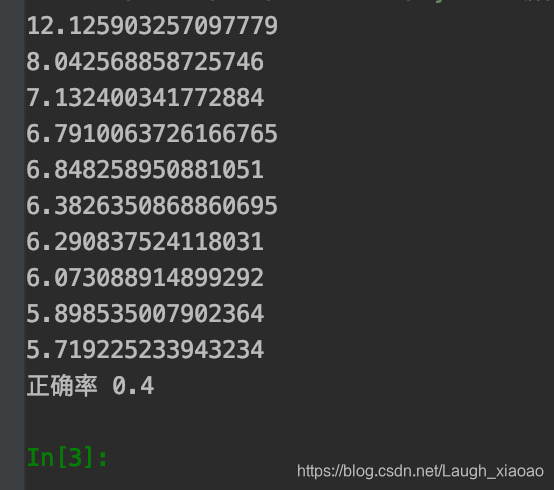
            print(loss)

        # 最后预测的部分
        output_data = softmax(np.matmul(testdata, weight))
        print(Accuracy(output_data, testlabels))

可以看到交叉熵确实再下降,但最后的正确率其实低的可怜,因为全都过拟合成2了.

总结

大致花费了一天的时间来考虑具体的梯度下降方法,在矩阵计算上卡了很久,但是总算解决了,还很菜,得继续加油…

参考文献

机器学习——softmax计算
Softmax求导及多元交叉熵损失梯度推导
梯度下降