牛客网-剑指offer

1. JZ1二维数组中的查找

思路：主要是关注右上角的元素，因为该元素是本行最大值，本列最小值，如果target大于该值，那么就需要在下面的行中查找。如果target小于该值，就需要在该列左边的列中查找。可以参考here

class Solution:
    # array 二维列表
    def Find(self, target, array):
        # write code here
        if isinstance(array, list):
            m = len(array)
        if len(array)>0 and isinstance(array[0], list):
            n = len(array[0])

        start_x, start_y = 0, 0 # 查询的开始位置
        end_x, end_y = m-1, n-1 # 查询的结束位置
        while start_x <= end_x and start_y <= end_y:
            right_top_x, right_top_y = start_x, end_y  # 右上角元素
            right_top_value = array[right_top_x][right_top_y]
            if right_top_value == target:
                return True     # 表示包含该整数
            elif right_top_value <= target:
                start_x += 1
            elif right_top_value >= target:
                end_y -= 1

        return False

2. JZ2替换空格

def replaceSpace(a):
    return s.replace(" ", "%20")

3. JZ3从尾到头打印链表

输入的是链表，将链表中的值保存到list中，然后逆向输出。

class ListNode:
    def __init__(self, x):
       self.val = x
       self.next = None

class Solution:
    # 返回从尾部到头部的列表值序列，例如[1,2,3]
    def printListFromTailToHead(self, listNode):
        # write code here
        a = listNode
        vals = []
        while a:
            vals.insert(0, a.val)
            a = a.next

        return vals

4. JZ4重建二叉树

思路：明确先序和中序中二叉树节点的顺序。先序遍历是：根左右，中序遍历是：左根右。因此，首先使用先序pre的第一个元素创建root节点，然后在中序tin中发现该元素对应的位置tin_i，使用tin_i左侧的内容构建为root的左子树，使用tin_i右侧的元素构建为root的右子数。

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution:
    # 返回构造的TreeNode根节点
    def reConstructBinaryTree(self, pre, tin):
        # write code here
        if len(pre)==0 or len(tin)==0:
            return None

        root = TreeNode(pre[0])     # 创建根节点
        for tin_i, tin_val in enumerate(tin):
            if root.val == tin_val: # 寻找tin中根节点所在位置
                root.left = self.reConstructBinaryTree(pre[1:tin_i+1], tin[:tin_i])
                root.right = self.reConstructBinaryTree(pre[tin_i+1:], tin[tin_i+1:])

                return root

5. JZ5用两个栈实现队列

思路：stack1用来存储push元素，而当要pop的时候，因为stack1属于栈，而队列的pop是队首元素，也就是stack1的栈底元素，因此需要借助stack2将stack1的元素倒过来存储在stack2中，此时直接删除stack2的栈顶元素即可。可参考牛客官方题解

即：push时，直接向stack1中加入元素；pop时存在两种情况，第一种是stack2为空，此时将stack1中的元素倒过来放入stack2中，然后删除stack2的栈顶元素；第二种是stack2不为空，直接删除stack2的栈顶元素即可。

# 下面这种使用python的list模仿栈的使用，如果使用python的特性，那么仅使用一个list就可以实现。
class Solution:
    def __init__(self):
        self.stack1 = []
        self.stack2 = []

    def push(self, node):
        # write code here
        self.stack1.append(node)
    def pop(self):
        if len(self.stack2) == 0:
            while len(self.stack1) >0:
                x = self.stack1.pop()
                self.stack2.append(x)
            return self.stack2.pop()
        else:
            return self.stack2.pop()

s = Solution()
s.push(1)
s.push(2)
s.push(3)
s.push(4)
print(s.stack1, s.stack2)
s.pop()
print(s.stack1, s.stack2)
s.push(5)
print(s.stack1, s.stack2)
s.pop()
print(s.stack1, s.stack2)

# 使用python的list特性，可以直接使用下面的代码实现。
class Solution:
    def __init__(self):
        self.stack1 = []

    def push(self, node):
        self.stack1.append(node)
    def pop(self):
        return self.stack1.pop(0)

6. JZ6 旋转数组的最小数字

题目描述：输入的是一个非递减数组的旋转（比如输入[3,4,5,1,2]，该数组是[1,2,3,4,5]这个数组的旋转)，输出旋转数组的最小元素，在这里也就是1.

思路：二分查找。参考牛客官方题解
难点：arr[mid]的比较对象。由于没有target，可以选择和端点比较，这里也就是右端点。
情形1：[3,4,5,1,2],此时arr[mid]=5, arr[right]=2,此时arr[mid]>arr[right],由于数组是非递减的的旋转数组，所以从[first,...,mid]是非递减的，因此，此时的最小值在[mid+1, right]这个范围。
情形2：[4,5,1,2,3],此时arr[mid]=1, arr[right]=3,此时arr[mid]< arr[right], 根据原数组是非递减的，因此可以确定最小值的范围是[left, mid]
情形3：[1,0,1,1,1],[1,1,1,0,1],这种情况时，不能很好地决定最小值所在的范围，因此每次让right-1来逐渐缩小范围。

class Solution:
    def minNumberInRotateArray(self, rotateArray):
        # write code here
        left = 0
        right = len(rotateArray)-1
        while left<right:
            mid = int((left+right)/2)
            if rotateArray[mid] > rotateArray[right]:
                left = mid + 1
            elif rotateArray[mid] < rotateArray[right]:
                right = mid
            elif rotateArray[mid] == rotateArray[right]:
                right -= 1
        return rotateArray[left]

7. JZ7 斐波那契数列

思路：第0项为0，第1项为1，之后的第2项为第0，1项之和，第n项为第n-2,n-1项之和。

class Solution:
    def Fibonacci(self, n):
        if n < 2:
            return n
        a = 0
        b = 1
        for i in range(1, n):   # 注意这里的range起始值。
            b, a = a+b, b
        return b

8. JZ8 跳台阶

思路：不管前面的怎么走，直接分析最后一步。比如台阶数目为n，那么最后一步可以是走2个台阶，也可以是走1个台阶，因此jumpFloor(n)=jumpFloor(n-1)+jumpFloor(n-2).

class Solution:
    def jumpFloor(self, number):
        if number <= 2:
            return number

        return self.jumpFloor(number-1)+self.jumpFloor(number-2)

但是这种方***超时，主要是重复计算比较多。因为在计算jumFloor(10)的时候，需要计算jumpFloor(9)和jumpFloor(8)，而计算jumpFloor(9)的时候又需要计算jumpFloor(8)等，因此考虑存储中间计算的结果。

# 另一种解决方法：
class Solution:
    def jumpFloor(self, number):
        if number <= 2:
            return number
        values = [-1 for i in range(number+1)]
        values[1] = 1
        values[2] = 2

        for i in range(3, number+1):
            values[i] = values[i-1] + values[i-2]
        return values[-1]

# 或者这样，此时就和斐波那契数列一致了。
class Solution:
    def jumpFloor(self, number):
        if number <= 2:
            return number
        a = 1
        b = 2

        for i in range(3, number+1):
            b,a = a+b, b
        return b

9. JZ9 变态跳台阶

思路：和每次跳1,2两个台阶没有本质不同。

class Solution:
    def jumpFloorII(self, number):
        # write code here
        if number <= 2:
            return number
        values = [-1 for i in range(number + 1)]
        values[1] = 1
        values[2] = 2

        for i in range(3, number + 1):
            values_i = 0
            for j in range(1, i):       # 当走有i个台阶时，存在的跳法就有从第1个台阶到第i-1个台阶的所有方法之和，
                # 然后加1，加1表示一次跳上i个台阶。
                values_i += values[j]
            values[i] = values_i + 1
        return values[-1]

10. JZ10矩形覆盖

思路：找规律。首先，当n=1是，只有1中方法；当n=2时，有2种方法；当n=3时，有3种方法。此时绘制出n=1,2,3时的图形可以发现，n=3时，相当于n=2时的情况，然后在右侧增加一个2*1的竖着的矩形；同时相当于n=1时，在右侧增加2个2*1的横着的矩形。如下图所示：

如上图，n=3是在n=1的基础上在右侧增加2个横着摆放的21的矩形框，在n=2的基础上在右侧增加1个竖着摆放的矩形框得到23的矩形框，因此f(n)=f(n-1)+f(n-2)
同理，当n=4时，是在n=2和n=3的基础上变化的。

注意：要求是n个2*1的小方块拼凑成2*n的矩形，也就是说高度都是2，因此只能横向增加长度。而竖着1个2*1的矩形可以达到高度2的要求，或者横着2个2*1的矩形可以达到高度2的要求。

# 在了解上述规律的基础上，就可以发现其实该题也就是和斐波那契数列一样了。
class Solution:
    def rectCover(self, number):
        # write code here
        if isinstance(number, int) and number <= 2:
            return number

        values = [0, 1, 2]
        for i in range(3, number+1):
            values.append(values[-1]+values[-2])

        return values[-1]

11. JZ11二进制中1的个数

原码、反码、补码知识：整数的原码、反码、补码是相同的。而负数的补码是符号位不变，其余各位取反，然后末尾加1得到。

Python中的整数是以补码的形式存储的，bin(负数)，输出的是它原码的二进制表示加上个负号，如下：

print(bin(10))  # 0b1010
print(bin(-10)) # -0b1010

注意：Python中的数是没有Overflow的，也就是没有位数限制。而补码是相对于位数来说的，比如32位的补码和16位的补码明显是不一样的，由于位数不定，因此要获取负数的补码，首先需要确定使用多少位来表示补码。

因此，通过将负数和0xffffffff进行与操作来获得对应的32位补码表示，然后使用bin函数将结果以二进制显示出来。如下：

print(-10 & 0xff, bin(-10 & 0xff))   # -10的16位补码246,对应的二进制格式为：0b11110110

在8位表示的整数中，-10的原码为1000 1010，保持最高位的1不变，剩余位取反，然后加1可以得到-10的补码：1111 0110。

在了解以上知识的基础上，本题的解题思路如下：

class Solution:
    def NumberOf1(self, n):
        # write code here
        print(bin(n), bin(n & 0xffffffff))
        if n >= 0:
            return bin(n).count('1')
        else:
            return bin(n & 0xffffffff).count('1')

换一个思路，主要是利用n&(n-1)，首先n&(n-1)的作用是：将n的二进制表示中最低位的1变为0。比如6的二进制表示为110，而7的二进制是在6的二进制基础上增加1，也就是111，因此当7&6时得到的就是110，也就是7的最低位的1会变为0。基于这个思想，就可以通过不断的&操作来实现计数的目的。

class Solution:
    def NumberOf1(self, n):
        count = 0
        while n & 0xffffffff != 0:
            count += 1
            n = n & (n - 1)
        return count

12. JZ12数值的整数次方

如果自己实现幂的效果，需要注意指数为负数的情况。

class Solution:
    def Power(self, base, exponent):
        if base == 0.0 and exponent == 0:
            return
        if base == 0.0:
            return 0
        if exponent == 0:
            return 1
        if exponent < 0:
            base = 1/base
            exponent = -exponent

        result = base
        for _ in range(1, exponent):
            result *= base
        return result

或使用python库文件math

class Solution:
    def Power(self, base, exponent):
        if base == 0.0 and exponent == 0:
            return
        import math
        return math.pow(base, exponent)

13. JZ13调整数组顺序使奇数位于偶数前面

思路：可以使用两个list，分别存储奇数和偶数，然后最终再合并起来，如下：

# -*- coding:utf-8 -*-
class Solution:
    def reOrderArray(self, array):
        # write code here
        odd = list()
        even = list()

        for i in array:
            if i % 2 == 0:
                even.append(i)
            else:
                odd.append(i)
        return odd+even

14. JZ14 链表中的第k个节点

思路：首先获取链表长度n，然后使用链表长度减去k，从而得到需要输出的节点的位置为n-k，然后顺着遍历一次即可。

class Solution:
    def FindKthToTail(self, head, k):
        len_node = 0
        p = head
        while p:
            len_node += 1
            p = p.next
        if k < 0 or k > len_node:
            return

        for i in range(len_node-k):
            head = head.next
        return head

15. JZ15 反转链表

思路：遍历pHead元素，然后在新链表p中使用头部插入的方式插入pHead中元素，从而达到逆序的效果。

# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    # 返回ListNode
    def ReverseList(self, pHead):
        # write code here
        p = ListNode(0)
        q = p
        while pHead:
            temp_node = ListNode(pHead.val)
            temp_node.next = q.next
            q.next = temp_node
            pHead = pHead.next

        return p.next

16. JZ16 合并两个排序的链表

思路：创建一个节点pHead3,然后通过迭代的方法来进行下面过程，当pHead1和pHead2当前所指向的位置不为空时，判断当前位置节点的值大小，将pHead3执行值比较小的节点，同时更新对应的指针即可。直到pHead1或者pHead2为空时，就将pHead3指向不为空的链表即可。

首先，链表初始化为：

接着，执行过程如下图，首先构建一个头结点，并pHead3,p3指向该结点；接着比较pHead1.val与pHead2.val的值大小：

1. if pHead2.val < pHead1.val，那么p3.next指向pHead2,然后pHead2后移，同时p3后移。比如下图中的①到②之间的变化过程。
2. 同理，if pHead1.val < pHead2.val。

最终，上图红线部分的元素所连接的就是pHead1和pHead2排序之后的结果（上图只是部分）。

class Solution:
    # 返回合并后列表
    def Merge(self, pHead1, pHead2):
        # write code here
        pHead3 = ListNode(-1)
        p3 = pHead3

        while pHead1 and pHead2:
            if pHead1.val < pHead2.val:
                p3.next = pHead1
                pHead1 = pHead1.next
                p3 = p3.next
            else:
                p3.next = pHead2
                pHead2 = pHead2.next
                p3 = p3.next

        if pHead1 == None:
            p3.next = pHead2
        else:
            p3.next = pHead1
        return pHead3.next

17. JZ17 树的子结构

思路：is_subtree是比较当前子树B与当前子树A是否为子树关系，而HasSubtree中需要不断的移动pRoot1指针来确定需要和B比较的部分。当pRoot1指向A树的根节点时，此时直接比较子树B是否为A的子树。如果不是，pRoot1指向A的左子树，然后比较B是否为pRoot1所指向的树的子树，如果不是，就将pRoot1指向A的右子树，然后比较B是否为pRoot1所指向的树的子树。
如下图：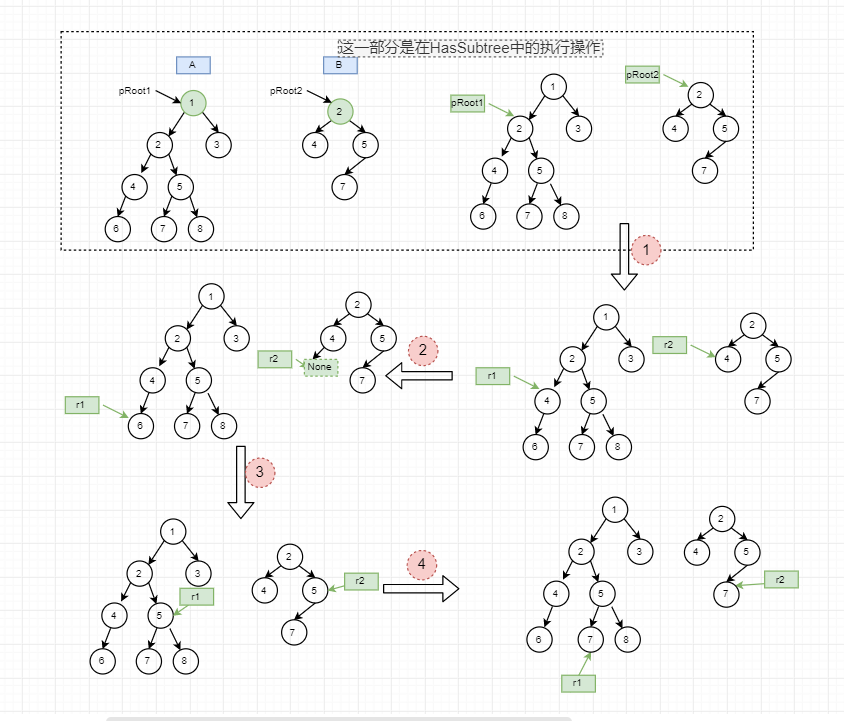

首先，在HasSubtree函数中会调用is_subtree发现B不是当前树的子树，所以pRoot1指向A的左子树，此时发现pRoot1.val=pRoot2.val，因此开始递归执行is_subtree来比较对应的左子树和右子树是否具有相同的值。

步骤1（如上图①，下同）：在is_subtree中，由于pRoot1和pRoot2对应值相等，所以此时比较左子树的值，这里使用r1和r2表示。
步骤2：接着比较r1和r2的左子树发现r2的左子树为None，此时可以断定r2的左子树是r1的子树，因此返回True
步骤3：然后比较r1和r2的右子树，发现值相等，均为5，接着继续比较右子树的左子树。
步骤4：此时值均为7，依然相等。
步骤5：...

# -*- coding:utf-8 -*-
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def HasSubtree(self, pRoot1, pRoot2):
        # write code here
        if not pRoot1:      # 如果A树为空，返回False
            return False
        if not pRoot2:      # 如果B树为空，返回False
            return False

        # 如果A树，B树都不为空，首先比较判断B树是否为A的子树
        is_B_A = self.is_subtree(pRoot1, pRoot2)
        if is_B_A:
            return True
        else:
            # 如果B树不是A的子树，此时判断B树是否为A的左子树的子树
            is_B_Aleft = self.HasSubtree(pRoot1.left, pRoot2)
            if is_B_Aleft:
                return True
            else:
                is_B_Aright = self.HasSubtree(pRoot1.right, pRoot2)
                if is_B_Aright:
                    return True
                else:
                    return False

    def is_subtree(self, r1, r2):
        if not r2:      # 如果r2为空，则表示当前r2位空，此时直接就返回True
            return True
        if not r1:      # 如果执行到这里，表示r2不为空，而r1为空，此时r2不可能与r1相等，此时直接返回False
            return False
        if r1.val == r2.val:    # 比较根节点是否相等，如果相等，就比较左右节点是否相等
            return self.is_subtree(r1.left, r2.left) and self.is_subtree(r1.right, r2.right)
        else:       # 如果根节点不相等，就直接返回False
            return False

考虑到上述代码中HasSubtree存在较多冗余，可以将HasSubtree修改为如下：

def HasSubtree(self, pRoot1, pRoot2):
        def HasSubtree(self, pRoot1, pRoot2):
        # write code here
        if not pRoot1:      # 如果A树为空，返回False
            return False
        if not pRoot2:      # 如果B树为空，返回False
            return False

        # 如果A树，B树都不为空，首先比较判断B树是否为A的子书
        is_B_A = self.is_subtree(pRoot1, pRoot2)
        if is_B_A:
            return True
        else:
            return self.HasSubtree(pRoot1.left, pRoot2) or self.HasSubtree(pRoot1.right, pRoot2)

18. JZ18 二叉树的镜像

思路：递归左右子树交换即可。
注意：在线平台中Mirror最终不需要返回值，直接输出的是root

# -*- coding:utf-8 -*-
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    # 返回镜像树的根节点
    def Mirror(self, root):
        # write code here
        if not root:
            return None

        if root.left:
            self.Mirror(root.left)
        if root.right:
            self.Mirror(root.right)
        root.right, root.left = root.left, root.right

19. JZ19顺时针打印矩阵。

思路：遍历的方向是按照右，下，左，上，右，下，左，上...的方向，因此定义direct来控制遍历的方向，使用flag来保存坐标点的是否被访问，通过边界判断和坐标点状态来改变下一次遍历的方向。如下图：

步骤1：向“右”遍历，到达4，此时到了边界，从而需要更改遍历方向为“下”。
步骤2：向“下”遍历，达到16，此时到达边界，从而更改遍历方向为“左”。
步骤3：向“左”遍历，达到13，此时到达边界，从而更改遍历方向为“上”。
步骤4：向“上”遍历，到达5，由于1已经遍历过，所以更改遍历方向为“右”。
步骤5：...

# -*- coding:utf-8 -*-
class Solution:
    # matrix类型为二维列表，需要返回列表
    def printMatrix(self, matrix):
        m = len(matrix)
        if m > 0:
            n = len(matrix[0])
        else:
            return

        direct = [(0, 1), (1, 0), (0, -1), (-1, 0)] # 控制遍历方向：右、下、左、上
        flag = [[0 for _ in range(n)] for i in range(m)]    # 保存访问状态
        res = []        # 保存要输出的数字

        point = (0, 0)  # 起始点的坐标
        i = 0           # 遍历方向索引
        res.append(matrix[point[0]][point[1]])  # res中插入起始点位置
        flag[point[0]][point[1]] = 1    # 表示坐标点已经访问

        count = 1       # 统计遍历次数，最大值为m*n，也就是矩阵元素个数
        while count < m*n:
            i = i % 4   # 求余循环遍历方向
            d = direct[i]
            new_point = (point[0]+d[0], point[1]+d[1])  # 新坐标点坐标

            # 边界判断和坐标点状态判断
            if new_point[1] >= n or new_point[0] >= m or new_point[1] < 0 or new_point[0] < 0 or flag[new_point[0]][new_point[1]] == 1:
                i += 1
                continue
            else:
                point = new_point   # 更新遍历坐标的位置
            res.append(matrix[point[0]][point[1]])
            flag[point[0]][point[1]] = 1
            count += 1
        return res

输入：[
    [1,2,3,4],
    [5,6,7,8],
    [9,10,11,12],
    [13,14,15,16]
]
输出：[1, 2, 3, 4, 8, 12, 16, 15, 14, 13, 9, 5, 6, 7, 11, 10]