CodeForces 559A Gerald's Hexagon(简单几何)

Description:

Gerald got a very curious hexagon for his birthday. The boy found out that all the angles of the hexagon are equal to . Then he measured the length of its sides, and found that each of them is equal to an integer number of centimeters. There the properties of the hexagon ended and Gerald decided to draw on it.
He painted a few lines, parallel to the sides of the hexagon. The lines split the hexagon into regular triangles with sides of 1 centimeter. Now Gerald wonders how many triangles he has got. But there were so many of them that Gerald lost the track of his counting. Help the boy count the triangles.

Input:

The first and the single line of the input contains 6 space-separated integers a1, a2, a3, a4, a5 and a6 (1 ≤ ai ≤ 1000) — the lengths of the sides of the hexagons in centimeters in the clockwise order. It is guaranteed that the hexagon with the indicated properties and the exactly such sides exists.

Output:

Print a single integer — the number of triangles with the sides of one 1 centimeter, into which the hexagon is split.

Sample Input:

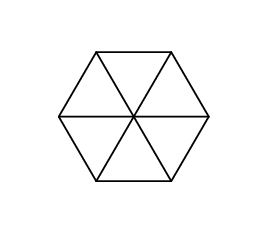
1 1 1 1 1 1

Sample Output:

6

Sample Input:

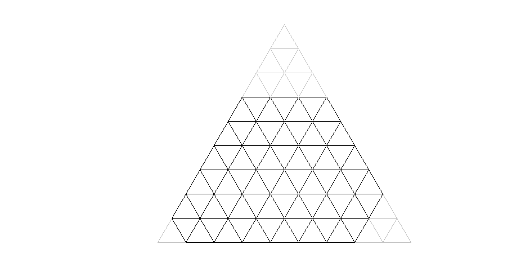
1 2 1 2 1 2

Sample Output:

13

Hint:

This is what Gerald’s hexagon looks like in the first sample:

And that’s what it looks like in the second sample:

题目链接

按顺时针顺序给出一个六个内角全部都是120°的六边形六条边的边长,求该六边形剖分成三条边边长全部为11的等边三角形的个数。

可以将这个六边形补全成为一个大三角形，大三角形中的小三角形数量 $n$n 与边长 $l$l 的关系为 $n=l^2$n=l2 ，再减去三个中等大小三角形中小三角形的数量即可。

AC代码:

#include<bits/stdc++.h>
using namespace std;

int main(int argc, char *argv[]) {
    int Len[6];
    for (int i = 0; i < 6; ++i) {
        scanf("%d", &Len[i]);
    }
    int Length = Len[0] + Len[1] + Len[2];
    int Ans = Length * Length;
    Ans -= Len[0] * Len[0];
    Ans -= Len[2] * Len[2];
    Ans -= Len[4] * Len[4];
    printf("%d\n", Ans);
    return 0;
}