CodeForces 794B Cutting Carrot(简单几何)

Description:

Igor the analyst has adopted n little bunnies. As we all know, bunnies love carrots. Thus, Igor has bought a carrot to be shared between his bunnies. Igor wants to treat all the bunnies equally, and thus he wants to cut the carrot into n pieces of equal area.
Formally, the carrot can be viewed as an isosceles triangle with base length equal to 1 and height equal to h. Igor wants to make n - 1 cuts parallel to the base to cut the carrot into n pieces. He wants to make sure that all n pieces have the same area. Can you help Igor determine where to cut the carrot so that each piece have equal area?

Input:

The first and only line of input contains two space-separated integers, n and h (2 ≤ n ≤ 1000, 1 ≤ h ≤ 105).

Output:

The output should contain n - 1 real numbers x1, x2, …, xn - 1. The number xi denotes that the i-th cut must be made xi units away from the apex of the carrot. In addition, 0 < x1 < x2 < … < xn - 1 < h must hold.
Your output will be considered correct if absolute or relative error of every number in your output doesn’t exceed 10 - 6.
Formally, let your answer be a, and the jury’s answer be b. Your answer is considered correct if .

Sample Input:

3 2

Sample Output:

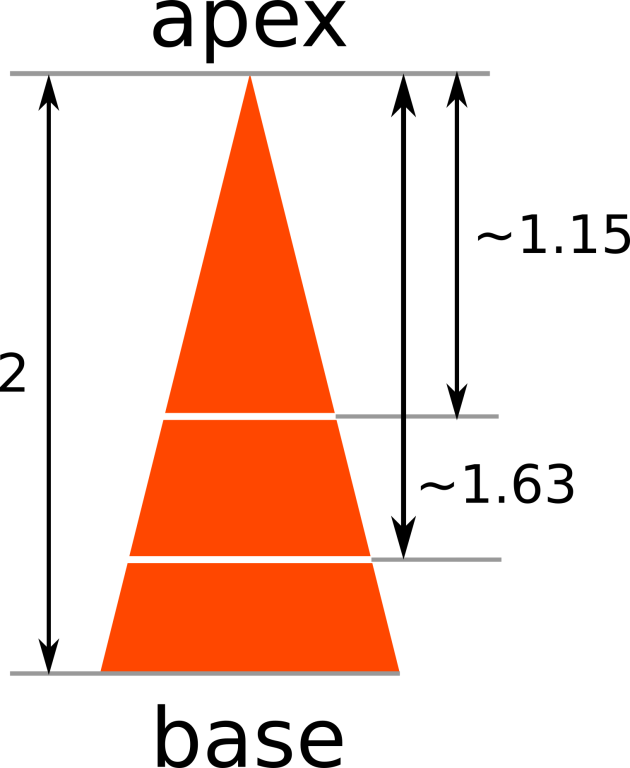
1.154700538379 1.632993161855

Sample Input:

2 100000

Sample Output:

70710.678118654752

题目链接

一个等腰三角形，底边长为 $1$1，高为 $h$h，作 $n-1$n−1条与底边平行的线将三角形分为面积相等的 $n$n份，求每条线距上顶点的距离。

三角形的总面积为 $\frac{h}{2}$2h​ ，若讲三角形分为面积相等的 $n$n份，设第一份三角形高为 $h_1$h1​ 底边长为 $a$a 则其的面积为 $\frac{a\times h_1}{2}$2a×h1​​，又等于 $\frac{h}{2}\times \frac{1}{n}$2h​×n1​，因为第一份三角形与完整三角形相似所以可得 $a=\frac{h_1}{h}$a=hh1​​，带入其面积公式可得方程 $h_1=h\times \sqrt{\frac{1}{n}}$h1​=h×n1​ ​ 通过此方程即可求得第一份三角形的高，同理可求得第二份三角形（第一份三角形＋梯形）的高为 $h_2=h\times \sqrt{\frac{2}{n}}$h2​=h×n2​ ​ ……

AC代码:

#include<bits/stdc++.h>
using namespace std;

int N, H;

int main(int argc, char *argv[]) {
    scanf("%d%d", &N, &H);
    for (int i = 1; i < N; ++i) {
        printf("%.12lf ", sqrt(double(i) / double(N)) * (double)H);
    }
    printf("\n");
    return 0;
}