换零钱问题--某条笔试真题01

首次感受互联网公司的氛围，没有想象中的高大上，不过感觉leader应该是个nice的人，分享几句印象颇深的话，行业决定你的下限，公司决定你的上限（选择很重要）；和优秀的人做有挑战的事；你永远也不可能准备好；你的成长速度和你解决的问题的难度正相关。
来还昨天的flag，今天就写第一道题吧。下面仅给出自己的答案，若有错误，还请批评指正。

一、兑换零钱
题目：现在有2元，3元，5元三种面值的硬币。给定数组arr，arr的长度等于3，每个元素分别代表各种硬币的数量，再给定一个整数aim代表要找的钱数，求组成aim的最小货币数。

输入样例：
aim = 20; arr = [3,4,5]
输出样例：
4

public class MinCoins_01 {
	public static int minCoins(int target, int[] arr) {
		if (arr == null) {
			return 0;
		}
		int min = Integer.MAX_VALUE;
		Boolean flag = false;
		for (int i = 0; i != arr[0]; i++) {
			int value = target - 2 * i;
			if (value < 0) {
				continue;
			}
			for (int j = 0; j != arr[1]; j++) {
				value = target - (2 * i + 3 * j);
				if (value < 0) {
					continue;
				}
				for (int k = 0; k != arr[2]; k++) {
					value = target - (2 * i + 3 * j + 5 * k);
					if (value < 0) {
						continue;
					}
					if (0 == value) {
						min = Math.min(min, i + j + k);
						flag = true;
					}
				}
			}
		}
		return flag ? min : -1;
	}
	public static void main(String[] args) {
		int aim = 18;
		int[] coins = { 2, 3, 5 };
		int[] coinNumber = { 5, 5, 5 };
		int result = minCoins(aim, coinNumber);
		System.out.println(result);
		System.out.println("Hello,Markov_Jin");
	}
}

思路：因为限定了每个硬币的使用数量，且只有3中面值的货币，可以暴力将这3个数排列的所有情况，选出满足和符合aim的组合，并比较出数量最小的组合。但是这样做显然复杂度较高，虽然每一次遍历都提前进行了剪枝，但仍然不是很好的解答。
看到这道题的时候我第一反应就是动态规划，左神的书上看到过，然而怎么也想不起来，最后只能老老实实暴力。下面我想分享一下动态规划的解法。原题中给定了每种硬币的数量，一定程度上减低了问题的难度，这样我们会想到遍历所有可能的数量，但是如果题目改为，每种面值的货币可以使用任意枚，那样就不能再指望我们的暴力出奇迹了。

用一个例子来讲解动态规划解法：
输入样例：
aim = 10; arr = [2,3,5]
输出样例：
4

思路：动态规划需要确定三要素：数组的行和列，数组中每个元素代表的含义，寻找数组前后之间的关系，利用问题的答案（一般在dp[n][n] 或者dp[0][0]）
大半夜突然脑洞大开，想谈谈我对动态规划的理解，简单的说就是记住你走过得每一个角落，当你想去下一个未曾去过的地方的时候，你就可以在你的记忆力找到你曾到过的距离未知地方最近的角落，举个脑洞更大的例子，比如你是LOL的盲僧，你曾在河道里打死过河蟹并随手在河道插了针眼，当你下次想去偷Buff的时候不知道哪条路最近的时候，你就可以直接传送到河道，去拿buff。
首先生成一个aim*arr.length(10x3)的二维数组dp[arr.length][aim]。
dp[i][j]：表示在可以任意使用arr[0…i]货币的情况下，组成j所需要的最小硬币数。本题中dp[1][2]代表着可以使用硬币{2，3}的情况下，组成aim=2所需要的最小硬币。dp[2][10] (使用硬币{2,3,5}组成aim=10的最小数组)就是我们要求解的答案，我们通过分析数组元素之间的关系利用左上方的dp[i’][j’]求解当前的dp[i][j]。

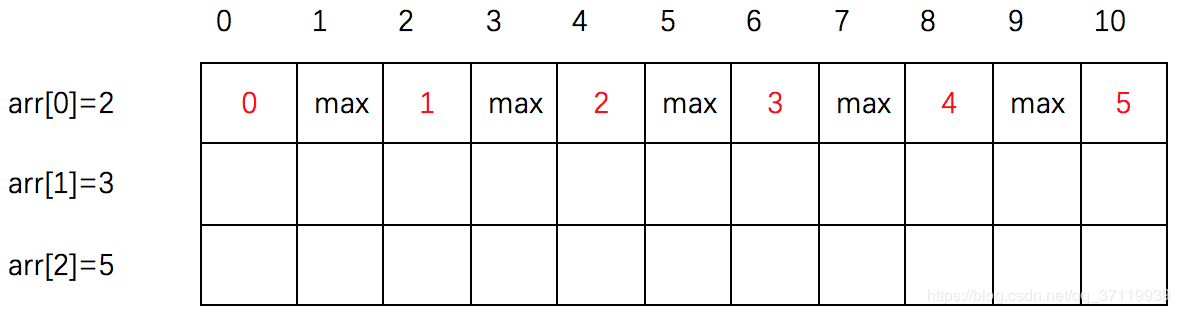
• 根据定义，先初始化数组中已知的部分元素。数组第一行dp[0][0…aim]表示只能使用arr[0]==2货币的情况下，找某个钱数需要的最少个数。此时只能找到的钱数是0元、2元、4元。。。10元。对应的最少货币数是0、1、2。。。5个，数组中对应的值dp[0][0]==0,dp[0][2]=1，。。。dp[0][5]=10。第一行的其他位置所代表的钱数则一律找不开，统一设为32位整数的最大数，如下图所示。
  
• 从第二行起，从左到右、从上到下计算。假设计算到位置(i,j)，dp[i][j]的可能值来自下面的情况。

1. 完全不使用当前arr[i],只使用arr[i-1]的最少货币数,即dp[i-1][j]的值。
2. 只用一张当前arr[i]的最少货币数,即dp[i-1][j-arr[i]]+1的值
3. 只用2张当前arr[i]的最少货币数,即dp[i-1][j-2*arr[i]]+2的值
4. 只用3张当前arr[i]的最少货币数,即dp[i-1][j-3*arr[i]]+3的值
...
上述所有的情况中，取值使用张数最小的情况。

用公式表示上面的所有情况：

$dp\left[i\right]\left[j\right]=min\left\{dp\right[i-1\left]\right[j-arr\left[i\right]\ast k]+k(k⩾0\};$dp[i][j]=min{dp[i−1][j−arr[i]∗k]+k(k⩾0};

$=min\left\{dp\right[i-1\left]\right[i]+[j-arr\left[i\right]\ast (k-0)]+k-0(k⩾0\};$=min{dp[i−1][i]+[j−arr[i]∗(k−0)]+k−0(k⩾0};

$=\>min\left\{dp\right[i-1\left]\right[j],dp[i-1\left]\right[j-arr\left[i\right]\ast x]+x\}(x⩾1\};$=>min{dp[i−1][j],dp[i−1][j−arr[i]∗x]+x}(x⩾1};

令x=y+1
$dp\left[i\right]\left[j\right]=\>min\left\{dp\right[i-1\left]\right[j],dp[i-1\left]\right[j-arr\left[i\right]-arr\left[i\right]\ast y]+y+1\}(y⩾0\};$dp[i][j]=>min{dp[i−1][j],dp[i−1][j−arr[i]−arr[i]∗y]+y+1}(y⩾0};

$dp\left[i\right][j-arr[i\left]\right]=min\left\{dp\right[i-1\left]\right[(j-arr[i\left]\right)-arr\left[i\right]\ast y]+y(y⩾0\}$dp[i][j−arr[i]]=min{dp[i−1][(j−arr[i])−arr[i]∗y]+y(y⩾0}

$dp\left[i\right]\left[j\right]=\>min\left\{dp\right[i-1\left]\right[j],dp[i\left]\right[j-arr\left[i\right]]+1\};$dp[i][j]=>min{dp[i−1][j],dp[i][j−arr[i]]+1};

dp[i][j]的值由其上方dp[i][j]和其左边的dp[i][j-arr[i]]确定，讨论这两种情况

• arr[0…i]组成j钱数j,要么不使用arr[i]，最小钱数为arr[0…i-1]组成j的钱数dp[i][j-arr[i]]，
• 要么使用arr[i]arr[i]，若arr[0…i]组成总钱数j-arr[i]的最小钱数存在(既能找开j-arr[i])，则找开总数j的最小钱数就是比j-arr[i]多使用一张面数为arr[i]的钱，所以找开总数j的最小钱数为dp[i][j-arr[i]]+1。
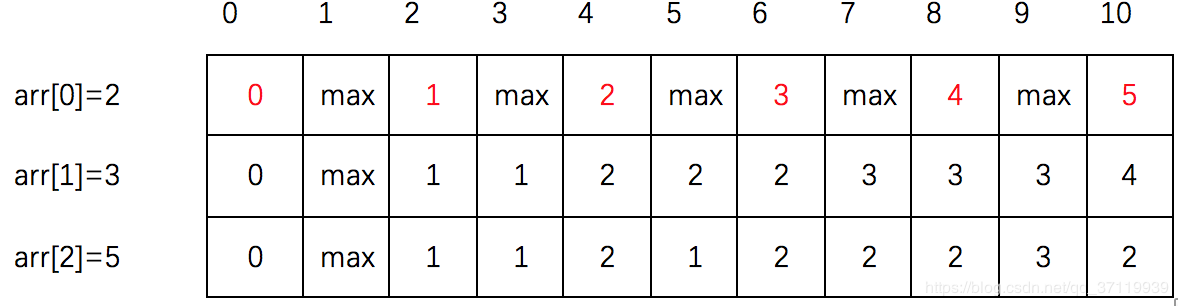
• 最后比较这两种情况的大小，选最小值,根据规律直接填满dp数组，最后一个元素dp[2][10]既是本题的解，[2,3,4]组成10的最小硬币数是2枚：即两枚5元的硬币。
  

public static int minCoins2(int target, int[] arr) {
		if (arr == null || arr.length == 0 || target < 0) {
			return 0;
		}
		int max = Integer.MAX_VALUE;
		int[][] dp = new int[arr.length][target + 1];
		// int value = -1;
		for (int i = 0; i != target + 1; i++) {
			dp[0][i] = max;
			if(j-arr[0]>0]&&dp[0][i-arr[0]!=max){
			dp[o][i]=dp[0][i-arr[0]+1
			}
			//dp[0][i] = i % arr[0] == 0 ? i / arr[0] : max;
		}
		int left = 0;
		for (int i = 1; i != arr.length; i++) {
			for (int j = 0; j != target + 1; j++) {
				left = max;
				if (j - arr[i] >= 0 && dp[i][j - arr[i]] != max) {
					left = dp[i][j - arr[i]] + 1;
				}
				dp[i][j] = Math.min(dp[i - 1][j], left);
			}
		}

		return dp[arr.length - 1][target] != max ? dp[arr.length - 1][target] : -1;
	}

此题的时间复杂度为O(N^2 * aim)，空间复杂度为O(N*aim).下次将补充空间复杂度将为O(aim)的算法。