跳跃【BFS】
From 牛客网:https://ac.nowcoder.com/acm/problem/25160
如题,bfs、dfs都可,后续补dfs版本。
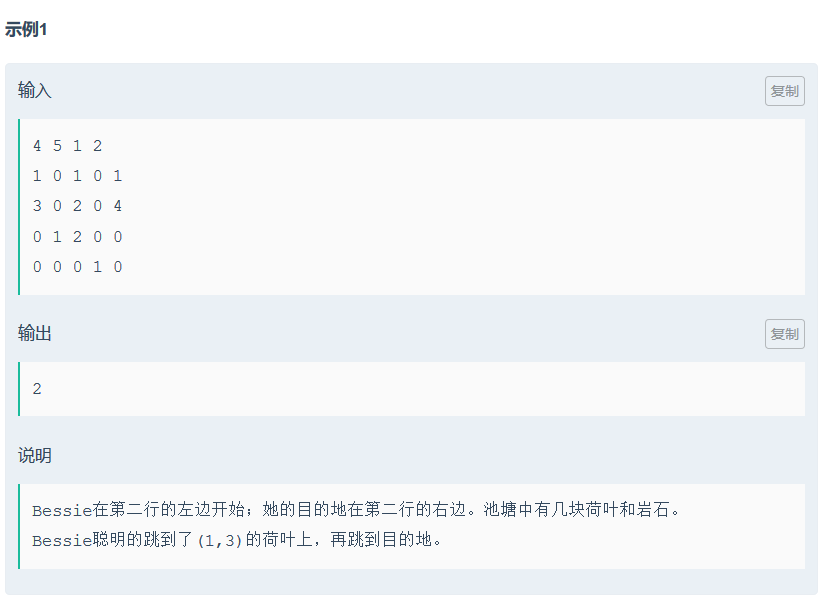
题意,从起点到终点,类似Chess中Knight的走法,即日字形,日字的长宽由m1,m2决定。且0为水不可踩,2为岩石不可踩。
思路:BFS向八个方向搜可走的格子,走过的点标记,结构体保存坐标和步数。由于BFS的特性,此题中先搜得目标时步数一定最小。所以当搜到时直接输出并return就可以了。
#include <bits/stdc++.h>
using namespace std;
int n,m;
int m1,m2;
int a[35][35];
int vis[35][35];
int f1,f2;
struct node{
int x,y,cnt;
};
queue <node> q;
void bfs(int x,int y)
{
// cout<<"x:"<<x<<" y:"<<y<<endl;
node now={x,y,0};
vis[x][y]=1;
q.push(now);
while(!q.empty())
{
int dr[8]={m1,m1,-m1,-m1,m2,m2,-m2,-m2};
int dc[8]={m2,-m2,m2,-m2,m1,-m1,m1,-m1};
node tmp=q.front();
q.pop();
//printf("tmp.x:%d tmp.y:%d cnt:%d\n",tmp.x,tmp.y,tmp.cnt);
//printf("f1:%d f2:%d\n",f1,f2);
if(tmp.x==f1&&tmp.y==f2)
{
printf("%d\n",tmp.cnt);
return ;
}
else
{
for(int i=0;i<8;i++)
{
node nxt=tmp;
int xx,yy;
xx=tmp.x+dr[i];
yy=tmp.y+dc[i];
//printf("nxt.x:%d nxt.y:%d a:%d\n",nxt.x,nxt.y,a[nxt.x][nxt.y]);
if(xx<n&&xx>=0&&yy<m&&yy>=0&&!vis[xx][yy]&&a[xx][yy]!=2&&a[xx][yy]!=0)
{
nxt.x=xx,nxt.y=yy;
//printf("nxt.x:%d nxt.y:%d a:%d\n",nxt.x,nxt.y,a[nxt.x][nxt.y]);
nxt.cnt++;
q.push(nxt);
vis[nxt.x][nxt.y]=1;
}
}
}
}
}
int main()
{
int x,y;
scanf("%d%d%d%d",&n,&m,&m1,&m2);
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
cin>>a[i][j];
if(a[i][j]==3)
{
x=i,y=j;
}
if(a[i][j]==4)
{
f1=i,f2=j;
}
}
}
//printf("f1:%d f2:%d\n",f1,f2);
bfs(x,y);
return 0;
}
 大疆公司氛围 169人发布
大疆公司氛围 169人发布


