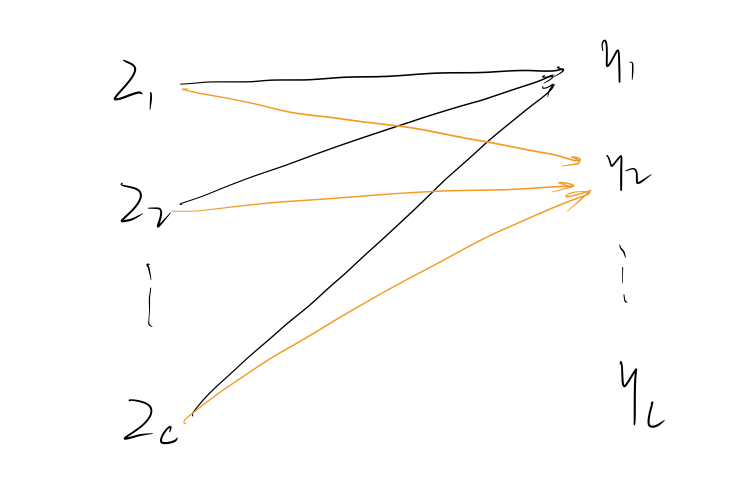softmax是一个多分类器，可以计算预测对象属于各个类别的概率。

公式

$y_i=S(z{)}_i=\frac{e^{z_i}}{\sum _{j=1}^C{e}^{z_j}}，i=1,...,C$yi​=S(z)i​=∑j=1C​ezj​ezi​​，i=1,...,C

• $z$z是上一层的输出，softmax的输入， 维度为 $C$C
• $y_i$yi​为预测对象属于第 $c$c类的概率

梯度

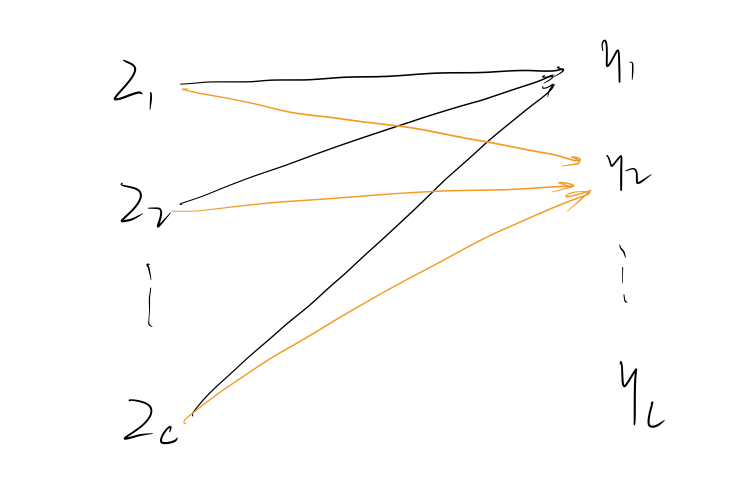
变量间的计算图如上，已知 $y$y的梯度 $\frac{\partial l}{\partial y_i},i=1,...,C$∂yi​∂l​,i=1,...,C，要计算 $z$z的梯度 $\frac{\partial l}{\partial z_j},j=1,...,C$∂zj​∂l​,j=1,...,C

从计算图中可以看到， $z$z的分量 $z_j$zj​对 $y$y的每一个分量都有贡献，因此：
$\frac{\partial l}{\partial z_j}=\sum _{i=1}^C\frac{\partial l}{\partial y_i}\frac{\partial y_i}{\partial z_j}$∂zj​∂l​=i=1∑C​∂yi​∂l​∂zj​∂yi​​

由于 $\frac{\partial l}{\partial y_i}$∂yi​∂l​已知，因此计算 $\frac{\partial y_i}{\partial z_j}$∂zj​∂yi​​即可！

为方便记 ${\sum }_{j=1}^C{e}^{z_j}$∑j=1C​ezj​为 ${\sum }_C$∑C​

（1） $i=j$i=j时：
$\begin{array}{cc}{\displaystyle \frac{\partial y_i}{\partial z_j}}& {\displaystyle =\frac{e^{z_i}\sum _C-e^{z_i}{e}^{z_i}}{{\sum _C}^2}}\\ {\displaystyle }& {\displaystyle =\frac{e^{z_i}}{\sum _C}-{\frac{e_{z_i}}{\sum _C}}^2}\\ {\displaystyle }& {\displaystyle =y_i-y_i^2}\\ {\displaystyle }& {\displaystyle =y_i(1-y_i)}\end{array}$∂zj​∂yi​​​=∑C​2ezi​∑C​−ezi​ezi​​=∑C​ezi​​−∑C​ezi​​​2=yi​−yi2​=yi​(1−yi​)​
（2） $i\ne j$i̸​=j
$\begin{array}{cc}{\displaystyle \frac{\partial y_i}{\partial z_j}}& {\displaystyle =\frac{0\sum _C-e^{z_i}{e}^{z_j}}{{\sum _C}^2}}\\ {\displaystyle }& {\displaystyle =-\frac{e_{z_i}}{\sum _C}\frac{e_{z_j}}{\sum _C}}\\ {\displaystyle }& {\displaystyle =-y_i{y}_j}\end{array}$∂zj​∂yi​​​=∑C​20∑C​−ezi​ezj​​=−∑C​ezi​​​∑C​ezj​​​=−yi​yj​​