Logistic 回归 损失函数推导及参数更新
Logistic 回归属于广义的线性模型,联系函数为sigmoid函数
广义的线性模型为 y=g(wTx+b),函数 g(.)起到了将线性回归模型预测值和真实标记联系起来的作用,称为“联系函数”(link function)。使得 g−1(y)与 wTx+b形成线性关系。
模型:
z=wTx+by=1+e−z1
损失函数推导:
采用极大似然估计来推导损失函数。
先写出正负样本的概率预测值:
p(y∗=1∣x;w,b)p(y∗=0∣x;w,b)=y=1−y
统一两个式子得到:
p(y∗∣x;w,b)=yy∗(1−y)1−y∗
假设样本独立且同分布,要让对每个样本的概率值更接近其所属分类,列出极大似然函数:
L(w;b)=i=1∏mp(yi∗∣xi,w,b)=i=1∏myiyi∗(1−yi)1−yi∗
取对数:
l(w,b)=i=1∑m[yi∗log(yi)+(1−y∗)log(1−yi)])
损失函数一般求最小值,因此
J(w,b)=−m1i=1∑m[yi∗log(yi)+(1−y∗)log(1−yi)]
正好是交叉熵损失函数
梯度推导
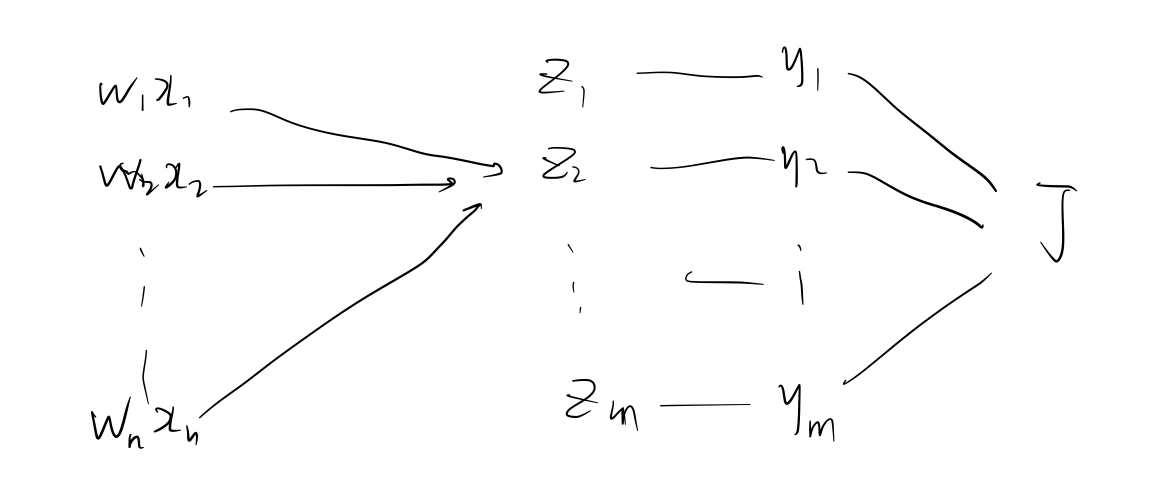
计算图
∂wj∂J=i=1∑m∂yi∂J∂zi∂yi∂wj∂zi
依次计算每一项
J(w,b)=−m1i=1∑m[yi∗log(yi)+(1−y∗)log(1−yi)]
∂yi∂J=−m1(yiyi∗−1−yi1−yi∗)=−m1(yi(1−yi)yi∗−yi)
y=1+e−z1
∂zi∂yi=(1+ez)2ez(1+ez)−ezez=yi(1−yi)
z=wTx+b
∂wj∂zi=xj
将三个导数计算结果代入上式,得到
∂wj∂J=i=1∑m−m1(yi(1−yi)yi∗−yi)⋅yi(1−yi)⋅xj=m1i=1∑m(yi−yi∗)xj
参数更新公式
wj=wj−α∂wj∂J=wj−αm1i=1∑m(yi−yi∗)xj