单纯形

web1web2web3web4web5

做题可以用画图分析图像来确定可行域来找最值。

写到程序里面，嘿嘿，你可以试试。

最大化

\(\sum\limits_{j=1}^{n} c_j*x_j\)

满足约束

\(\sum\limits_{j=1}^{n} c_{i,j}*x_j <= b_i i=1,2……m\)

\(x_i >= 0 i=1,2……m\)

变一下

最大化

\(\sum\limits_{j=1}^{n} c_j*x_j\)

满足约束

$ x_{i+n} = b_i - \sum\limits_{j=1}^{n} c_{i,j}*x_j i=1,2……m $

\(x_i >= 0 i=1,2……n+m\)

每次找 \(c_j\) 是正数的项给找出来。

用其他约束条件(约束最紧的)替换掉，叫做转轴。

直到每个 \(c_j\) 都是负数

最后的答案就是那个最大化式子的常数项。

如果初始值的 \(b < 0\) 那么还需要一些操作，具体参见web1

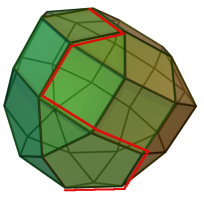
线性规划的约束画在坐标系里就是一个凸多面体，

可行解就是这个凸多面体的内点，

将目标函数（超平面）往多面体上靠，

第一个切点就是一个最优解，

因此多面体的顶点中一定会出现最优解。

每次从单纯形上的一个顶点走到一个更好的顶点直到找到最小（大）值。

大概就是这个意思吧

复杂度 \(O(一两百)\)

结合着uoj上的注释还是挺明白的

不过uoj代码我感觉随随便便就能过98，感觉不靠谱